Прогнозирование по моделям парной линейной регрессии

Пусть мы построили выборочную линейную регрессионную модель с двумя переменными и оценили параметры методом наименьших квадратов. Если наша модель адекватна, то мы можем находить прогнозные значения зависимой переменной Y исходя из построенной выборочной модели. При этом мы можем получить два типа прогнозов: точечные и интервальные (рис.3.6).

Точечный прогноз – это оценка истинного отдельного значения зависимой переменной для прогнозного значения по построенной выборочной модели:

. (3.13)

Точечный прогноз дает значение зависимой переменной для соответствующего значения объясняющей переменной по построенной выборочной модели.

Рис.3.6. Графическая интерпретация точечного и интервального прогноза по модели парной линейной регрессии

При этом истинное значение для прогнозного значения будет равно

, (3.14)

где

- ненаблюдаемое значение случайной величины в (n+1) периоде.

Истинное значение Y мы найти не можем, а можем лишь оценить его с помощью прогноза. Поэтому прогнозное значение является оценкой истинного отдельного значения .

Таким образом, по нашей выборочной модели мы легко можем находить прогнозное значение зависимой переменной. Уточним, что такое прогнозное значение будет точечным.

Исходя из полученного точечного прогноза, мы можем построить доверительный интервал для истинного отдельного значения зависимой переменной, т.е. построить интервал, в который с определенной заданной вероятностью попадает действительное значение зависимой переменной. Такой доверительный интервал при заданном уровне возможной ошибки a·100% для будет находиться по формуле

(3.15)

где

;

- оценка стандартной ошибки оценивания;

n - количество наблюдений в выборке;

- прогнозное значение Х;

- наблюдаемые значения Х;

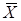- среднее по выборке значение Х.

Таким образом, формула (3.15) дает нам доверительный интервал для истинного отдельного значения зависимой переменной.

Интервальный прогноз – это доверительный интервал для истинного отдельного прогнозного значения зависимой переменной при заданном уровне возможной ошибки a·100%.

Как видно из (3.15), доверительный интервал прогноза минимальный при и увеличивается нелинейно по мере того, как удаляется от своего среднего по выборке значения .

Считается, что период прогнозирования должен быть по крайней мере в 3 раза короче, чем тот период, для которого было оценено уравнение регрессии.

На практике более важным является построение доверительного интервала для математического ожидания , т.е. построение доверительного интервала для

, (3.16)

т.к., собственно говоря, нет большого смысла прогнозировать точное значение , учитывая случайный характер .

В этом случае формула (3.15) несколько модифицируется и доверительный интервал для при a·100% уровне возможной ошибки имеет вид:

(3.17)