Множественная линейная регрессия

Далее мы будем говорить о линейной зависимости Y от вектора Х, то есть о множественной линейной регрессии. Теоретическое уравнение модели множественной линейной регрессии имеет вид:

, (3.18)

где

m - число объясняющих переменных (факторов);

b - вектор неизвестных параметров размерности k (в модели (3.18) ).

Пусть имеется n наблюдений вектора Х и зависимой переменной Y.

Для того чтобы формально можно было решить задачу, то есть найти некоторый наилучший вектор параметров, должно быть .

Случай 1. Если (например, при двух объясняющих переменных в уравнении и трех наблюдениях), то оценки параметров b рассчитываются единственным образом – путем решения системы линейных уравнений

{ ; i=(1, 2,..., n) - индекс наблюдения}.

Так, через три точки-наблюдения в трехмерном пространстве можно провести единственную плоскость, определяемую параметрами .

Случай 2. Если число наблюдений больше минимально необходимого, то есть 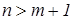, то уже нельзя подобрать линейную формулу, в точности удовлетворяющую всем наблюдениям, и возникает необходимость оптимизации, то есть выбора наилучшей формулы-приближения для имеющихся наблюдений. Положительная разность 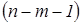в этом случае называется числом степеней свободы. Если число степеней свободы мало, то статистическая надежность оцениваемой формулы невысока. Так, если проведена плоскость «в точности» через имеющиеся три точки наблюдений, любая четвертая точка-наблюдение из той же генеральной совокупности будет практически наверняка лежать вне этой плоскости, возможно – достаточно далеко от нее.

Обычно при оценке множественной регрессии для обеспечения статистической надежности требуется, чтобы число наблюдений по крайней мере в 3 раза превосходило число оцениваемых параметров.

Задача построения множественной линейной регрессии состоит в нахождении k -мерного вектора , элементы которого есть оценки соответствующих элементов вектора b. Критерии оценивания, как и в случае парной регрессии, могут быть различными; мы будем вновь использовать метод наименьших квадратов (МНК).

Уравнение модели с оцененными параметрами имеет вид

, (3.19)

где

e - отклонения наблюдаемых значений зависимой переменной Y от теоретической линии регрессии.

В соответствии с идеей метода наименьших квадратов критерием для нахождения вектора является .

Проблема здесь состоит не только в том, чтобы объяснить возможно большую долю колебаний переменной Y, но и отделить влияние каждого из факторов, рассматриваемых как объясняющие переменные.

При выполнении предположений (предпосылок) относительно ошибок, оценки параметров множественной линейной регрессии, полученные МНК, являются несмещенными, состоятельными и эффективными.

Для анализа статистической значимости полученных оценок параметров множественной линейной регрессии необходимо (как и в случае парной регрессии):

1) оценить дисперсию и стандартные отклонения оценок параметров ;

2) для проверки нулевой гипотезы для оценки каждого из параметров рассчитать t-статистику:

,

имеющую распределение Стьюдента с степенями свободы;

3) сопоставить с критическим значением распределения Стьюдента . Если , то с принятым уровнем доверия оценка j -того параметра статистически достоверно отличается от нуля (является значимой).

Общее качество регрессионной модели обычно анализируется с помощью коэффициента детерминации .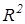

Для определения статистической значимости коэффициента детерминации 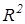рассчитывается F-статистика:

.

В предположении выполнения предпосылок относительно ошибок, величина F-статистики имеет распределение Фишера с степенями свободы, где m – число объясняющих переменных, k – число оценённых параметров, n – число наблюдений.

F=0 равнозначно тому, что величина Y статистически независима от вектора Х (т.е. между вектором Х и величиной Y отсутствует значимая функциональная связь).

Поэтому проверяется нулевая гипотеза для F-статистики о равенстве нулю одновременно всех коэффициентов линейной регрессии, за исключением свободного члена, для чего при заданном уровне значимости и числе степеней свободы по таблицам распределения Фишера находится критическое значение 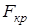, и нулевая гипотеза отвергается, если .

Распределение Фишера может быть использовано не только для проверки гипотезы об одновременном равенстве нулю всех коэффициентов линейной регрессии, за исключением свободного члена, но и гипотезы о равенстве нулю части этих коэффициентов. Это позволяет оценить обоснованность исключения отдельных переменных или их групп из числа объясняющих переменных, или же, наоборот, включения их в это число.

Оценка обоснованности исключения переменных из числа объясняющих

Пусть, например, вначале была оценена множественная линейная регрессия

по n наблюдениям с m объясняющими переменными и k параметрами, и коэффициент детерминации равен .

Затем последние s переменных исключены из числа объясняющих, и по тем же данным оценено уравнение

,

для которого коэффициент детерминации равен (он обязательно уменьшился, поскольку каждая дополнительная переменная объясняет пусть небольшую, но часть вариации зависимой переменной).

Для того чтобы проверить гипотезу об одновременном равенстве нулю всех коэффициентов регрессии, находящихся при исключенных из модели объясняющих переменных, рассчитывается F-статистика

,

имеющая распределение Фишера с 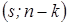степенями свободы.

По таблицам распределения Фишера, при заданном уровне значимости и степенях свободы 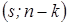, находится критическое значение F-статистики, и если рассчитанное значение F-статистики превосходит критическое, то нулевая гипотеза отвергается. В таком случае исключать сразу из числа объясняющих все s переменных некорректно.

Пояснения. F-статистика оказывается относительно большой, если велика разность . В этом случае исключение данного набора s объясняющих переменных приводит к слишком большому сокращению доли объясненной дисперсии зависимой переменной, и поэтому недопустимо. Если, наоборот, эта доля сокращается незначительно, то F-статистика невелика, нулевая гипотеза не отвергается, и указанные s переменных могут быть исключены из уравнения регрессии.

Оценка обоснованности включения новых объясняющих переменных

Аналогичные рассуждения проводятся и по поводу обоснованности включения в уравнение регрессии новых объясняющих переменных. В этом случае рассчитывается F-статистика ( – коэффициент детерминации регрессии с новыми объясняющими переменными):

,

имеющая распределение , и если она превышает критический уровень, то включение новых переменных объясняет существенную часть необъясненной ранее дисперсии зависимой переменной Y. Отметим лишь, что добавлять новые переменные целесообразно, как правило, по одной.

Другой подход.

В вопросе о добавлении объясняющих переменных в уравнение регрессии полезным может оказаться рассмотрение коэффициента детерминации с поправкой на число степеней свободы (для получения несмещенных оценок дисперсии):

.

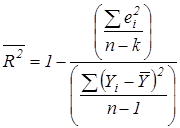В числителе дроби, которая вычитается из единицы, стоит сумма квадратов отклонений наблюдений 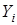от теоретической линии регрессии, в знаменателе – сумма квадратов отклонений наблюдений 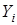от среднего по выборке значения зависимой переменной Y.

Обычный 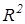(без поправки) рассчитывается по формуле

и всегда растет при добавлении новой объясняющей переменной.

В (с поправкой) растет величина k, уменьшающая его. Если увеличение доли объясненной дисперсии при добавлении новых объясняющих переменных мало, то (с поправкой) может уменьшиться. Если это так, то добавлять новые объясняющие переменные нецелесообразно.

Проверка гипотезы о совпадении уравнений регрессии для отдельных групп наблюдений (тест Чоу)

F-статистика Фишера используется также для проверки гипотезы о совпадении уравнений регрессии для отдельных групп наблюдений, что важно для ответа на вопрос: можно ли за весь рассматриваемый в модели интервал построить единое уравнение регрессии, или же нужно разбить его на части и на каждой из частей строить своё уравнение регрессии (рис.3.7).

Пусть имеются две выборки, содержащие, соответственно, n₁ и n₂ наблюдений. Для каждой из этих выборок оценено одно и то же уравнение регрессии вида

.

Пусть суммы квадратов отклонений 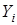от теоретической линии регрессии равны для них соответственно S₁ и S₂.

Пусть оценено уравнение регрессии того же вида сразу для всех (n₁+n₂) наблюдений и сумма квадратов отклонений 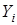от теоретической линии регрессии равна для него S₀.

Проверяется нулевая гипотеза, заключающаяся в том, что все соответствующие коэффициенты этих уравнений равны друг другу, то есть что уравнение регрессии для этих выборок одно и то же.

Тогда рассчитывается F-статистика по формуле

.

Она имеет распределение Фишера с степенями свободы.

F-статистика будет близкой к нулю, если уравнение регрессии для обеих выборок одинаково, поскольку в этом случае . Если же ее расчетное значение велико (то есть больше критического значения при данном уровне значимости), то нулевая гипотеза отвергается.

Рис.3.7. К проверке гипотезы о совпадении уравнений регрессии для отдельных групп наблюдений