Несовершенная мультиколлинеарность

На практике совершенная мультиколлинеарность встречается исключительно редко.

Несовершенная мультиколлинеарность, то есть стохастическая связь объясняющих переменных, характеризуется величиной коэффициента корреляции между объясняющими переменными.

Чем ближе по абсолютной величине значение коэффициента корреляции к единице, тем ближе мультиколлинеарность к совершенной и тем труднее разделить влияние коррелированных объясняющих переменных на поведение зависимой переменной, и тем менее надежными будут оценки параметров регрессии при этих переменных.

План действий

В общем случае:

1) если при оценивании уравнения регрессии по данным выборки несколько факторов оказались незначимыми, то нужно выяснить, нет ли среди них сильно коррелированных между собой. Для этого полезно построить корреляционную матрицу, в которую включены факторы и зависимая переменная. В модель необходимо в первую очередь включать факторы, которые коррелируют с зависимой переменной и не коррелируют между собой. Существует много методов исследования мультиколлинеарности. Наиболее полно исследовать мультиколлинеарность можно с помощью метода Феррара-Глобера.

При наличии межфакторной корреляции один из пары связанных между собой факторов исключается, либо в качестве объясняющего фактора берется какая-то их функция;

2) если же незначимым оказался только один фактор, то его можно исключить или заменить другим (хотя, возможно, на каком-то более коротком промежутке времени данный фактор оказался бы значимым).

Наиболее характерные признаки мультиколлинеарности:

1. Небольшое изменение исходных данных (например, добавление новых наблюдений) приводит к существенному изменению оценок параметров модели.

2. Оценки параметров имеют большие стандартные ошибки, малую значимость, в то время как модель в целом является значимой (высокое значение коэффициента детерминации и соответствующей F‑ статистики).

3. Оценки параметров имеют неправильные с точки зрения теории знаки или неоправданно большие значения.

Принципиальное замечание: оценка любой множественной регрессии будет страдать от мультиколлинеарности в определенной степени, если только все объясняющие переменные не окажутся абсолютно некоррелированными. Поэтому рассмотрение данной проблемы начинается только тогда, когда это серьезно влияет на результаты оценки регрессии, т.е. когда получены неудовлетворительные оценки параметров регрессии.

Методы, которые могут быть использованы для смягчения мультиколлинеарности, делятся на две категории:

1. Повышение степени выполнения условий, обеспечивающих надежность оценок параметров регрессии.

2. Использование внешней информации.

Первая категория методов

t-статистика для оценки i -того параметра рассчитывается по формуле:

.

Оценка параметра является статистически значимой, если 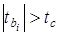. Отсюда – возможные пути обеспечения надежности оценок параметров:

- увеличение ;

- уменьшение .

Во-первых, если имеется возможность, то для сведения к минимуму теоретической дисперсии оценок параметров регрессии было бы полезным увеличить число наблюдений (увеличить размер выборки) и тем самым повысить точность оценок параметров регрессии.

Во-вторых, столь же важно максимизировать выборочные дисперсии объясняющих переменных: чем больше , тем меньше дисперсия . Поэтому желательно выбирать таким образом, чтобы их разброс вокруг среднего по выборке значения был большим.

В третьих, можно сократить величину оценки дисперсии ошибок .

Случайная ошибка модели включает в себя объединенный эффект всех переменных, оказывающих влияние на величину Y, которые не включены явно в уравнение регрессии. Если допустить мысль о том, что важная переменная могла быть опущена и, следовательно, оказывает влияние на ошибку, то можно сократить величину , если добавить эту переменную в уравнение регрессии.

Если, однако, новая переменная линейно связана с одной или несколькими переменными, уже включенными в уравнение, то ее введение может еще больше усугубить проблему мультиколлинеарности.

Таким образом, если число наблюдений и выборочные дисперсии объясняющих переменных велики, а дисперсия случайной ошибки мала, то в итоге можно получить вполне хорошие оценки.

Вторая категория методов

Существует два типа внешней информации: теоретические ограничения и внешние эмпирические оценки.