Пример 5.4.

Требуется построить функцию спроса:

, (5.3)

где

- спрос на товар в момент времени t;

- цена товара в момент времени t;

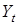- личный доход в момент времени t;

- случайная ошибка.

Но имеется проблема мультиколлинеарности, т.к. располагаемый личный доход и цена имеют ярко выраженные временные тренды, а, следовательно, тесно коррелированы.

Предположим, однако, что также имеются пространственные (перекрестные) статистические данные для спроса и дохода , полученные из другой выборки.

Если допустить, что все конечные потребители (домохозяйства) в проводимом анализе платили за данный товар одинаковую цену, то можем построить модель “спрос-доход”:

. (5.4)

Получив оценку для при оценивании регрессионной зависимости от (5.4), подставим ее вместо в уравнение (5.3).

Теперь определяется новая переменная , равная , описывающая спрос, скорректированный на изменения дохода.

После этого модель (5.3) принимает вид:

.

Рассчитав для каждого наблюдения, мы оцениваем регрессионную зависимость скорректированного спроса от цены товара , и, так как здесь имеется только одна независимая переменная, мультиколлинеарность автоматически исключается.

При использовании этого метода могут возникнуть 2 проблемы, которые необходимо учитывать.

Во-первых, оценка величины зависит от точности оценки величины , которая безусловно, подвержена влиянию ошибки выборки.

Во-вторых, мы допускаем, что коэффициент при доходе имеет одинаковый смысл для случаев временных рядов ( в модели (5.3)) и перекрестных выборок ( в модели (5.4)), что, конечно, может быть и не так. Для большинства товаров краткосрочная и долгосрочная эластичность спроса по доходу может значительно различаться.

Одна из причин этого состоит в том, что характер расходов подвержен влиянию инерции, которая в краткосрочном периоде может превзойти эффекты дохода.

Другая причина заключается в том, что изменение уровня дохода может оказать на расходы как непосредственное (в виде изменения бюджетного ограничения), так и косвенное влияние (за счет изменения образа жизни), причем косвенное влияние происходит намного медленнее, чем прямое. В качестве первого приближения обычно считается, что регрессии для временных рядов, особенно с небольшими периодами выборки, дают показатели краткосрочной эластичности, в то время как регрессии с использованием данных перекрестных выборок дают показатели долгосрочной эластичности.