Причины возникновения гетероскедастичности

Гетероскедастичность может быть следствием разных причин.

1.Довольно часто гетероскедастичность возникает, если анализируемые объекты, говоря нестрого, неоднородны (сильно отличаются один от другого). Например, если исследуется зависимость прибыли предприятия от каких-либо факторов, скажем, от размера основных фондов, то естественно ожидать, что для больших предприятий колебание прибыли будет выше, чем для малых.

2.Возможны ошибки и неточности в исходных данных (ошибки измерения). Часто бó льший разброс наблюдается при больших значениях зависимой переменной. Если в данных содержится значительная ошибка, то, естественно, большим будет и отклонение, рассчитанное по ошибочным данным.

Для того чтобы избавиться от гетероскедастичности, необходимо наблюдениям с наименьшими дисперсиями придать наибольшие веса, а с максимальными дисперсиями – наименьшие. При известных для каждого наблюдения значениях дисперсии ошибок 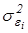эта идея реализована в методе взвешенных наименьших квадратов, именуемом также взвешенный МНК, или обобщенный МНК.

Метод взвешенных наименьших квадратов (Взвешенный МНК)

Рассмотрим процедуру оценивания параметров для парной линейной регрессионной модели с гетероскедастичностью:

.

Преобразуем эту модель, разделив каждое наблюдение на соответствующее ему значение стандартного отклонения :

, (5.5)

где .

Для преобразованной модели (5.5) условия гомоскедастичности выполнены, так как 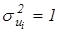. Применяя к (5.5) обычный метод наименьших квадратов, оценки параметров получим минимизацией суммы взвешенных квадратов отклонений:

. (5.6)

Содержательный смысл такого подхода.

Используя обычный МНК, мы минимизируем сумму квадратов отклонений

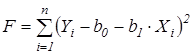, (5.7)

в которую, говоря нестрого, разные слагаемые дают разный статистический вклад из-за различной дисперсии, что в конечном итоге и приводит к неэффективности МНК-оценки. “Взвешивая” каждое наблюдение с помощью коэффициента , мы устраняем такую неоднородность: наблюдениям с бó льшей дисперсией придается меньший вес . Оценки МНК параметров преобразованной модели дают непосредственно оценки исходной модели.

При использовании взвешенного МНК оценки параметров не только получаются несмещенными (они будут таковыми и для обычного МНК), но и более точными (имеют меньшую дисперсию), чем невзвешенные оценки.

Ключевым моментом при применении метода взвешенных наименьших квадратов является выбор весов.