Предпосылки к выбору весов

1. На практике дисперсии ошибок 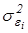неизвестны, поэтому их заменяют оценками . Тогда модель (5.5) примет вид:

. (5.8)

После замены переменных, обычным МНК оценивается преобразованная модель вида:

, (5.9)

для которой значения преобразованных переменных вычисляются по формулам .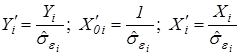

При оценивании параметров модели (5.9) следует иметь ввиду, что в модели (5.9) отсутствует свободный член.

2. Число оценок дисперсии ошибок равно “ n ”. Проблема заключается в том, что без дополнительных ограничений невозможно получить приемлемые оценки дисперсии ошибок.

Рассмотрим некоторые примеры наложения таких ограничений:

1. В первом приближении веса могут устанавливаться пропорционально остаткам невзвешенной регрессии.

2. Для экономических данных стандартные отклонения ошибок 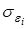часто пропорциональны значениям объясняющей переменной , т.е. . Тогда модель (5.8) примет вид:

. (5.10)

После замены переменных, обычным МНК оценивается преобразованная модель вида:

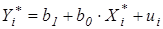, (5.11)

для которой значения преобразованных переменных вычисляются по формулам . Заметим, что параметры и 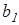поменялись ролями: коэффициент при будет эффективной оценкой параметра , а свободный член – эффективной оценкой параметра 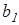исходной модели.

3. При построении множественной линейной регрессии в некоторых ситуациях априорно можно считать, что ошибка прямо пропорциональна одной из независимых переменных, например :

.

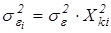Тогда, разделив i -тое уравнение на , i=1,..., n (n – количество наблюдений), и вводя новые независимые переменные и новую зависимую переменную , i=1,..., n, j=1,..., m (m – число независимых переменных), получим классическую регрессионную модель. МНК-оценки параметров этой модели дают непосредственно оценки параметров исходной модели.

4. Может оказаться целесообразным предположить, что не стандартные отклонения ошибок, а дисперсии ошибок пропорциональны значениям , т.е. .