Предел функции в точке

Предел функции

Предел функции в точке

Определение. Точка называется предельной точкой области определения 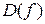, если в любой ее окрестности содержатся точки из области определения, отличные от нее самой.

Пусть точка является предельной точкой области определения, .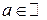

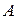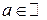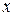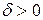Определение. Число называется пределом функции в точке (или «при , стремящемся к »), если для любого числа существует число такое, что неравенство

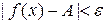
выполняется для всех 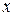, для которых .

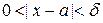Комментарий к определению. Любую близость к 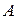можно достичь, приближая 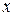к . Сложность формулировки определения вызвана необходимостью точно указать смысл выражений «значения аргумента 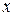, близкие к » и «значения функции близки к ».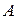

Обозначение: 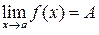или .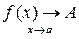

Пример 1. Если , то ,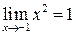

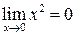
Пример 2. Если 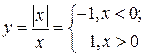, то 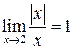, , 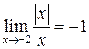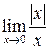не существует

Пример 3. . , .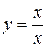

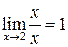Запись определения предела с использованием символов математической логики выглядит так:

.

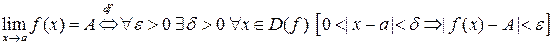Определение предела можно переписать и в другом виде.

.

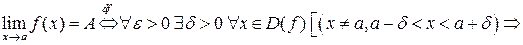
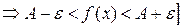Это определение также можно записать в окрестностной форме.

.
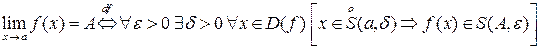