
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства функций, имеющих пределы
|
|
Теорема 1. (единственность предела). Если функция  имеет предел
имеет предел 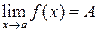 (
( ), то это предел единственный.
), то это предел единственный.
Теорема 2. (необходимое условие существования предела). Если функция  имеет конечный предел при
имеет конечный предел при  , то она ограничена в некоторой окрестности точки
, то она ограничена в некоторой окрестности точки  .
.
Теорема 3. Если функция  имеет конечный предел при
имеет конечный предел при  равный
равный 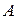 и
и  , то существует проколатая окрестнось точки
, то существует проколатая окрестнось точки  такая, что для любого
такая, что для любого 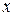 из этой окрестности будет выполняться неравенство
из этой окрестности будет выполняться неравенство  .
.
Теорема 4. Пусть в некоторой окрестности  имеет место неравенство
имеет место неравенство  . Тогда если существуют конечные пределы
. Тогда если существуют конечные пределы  и
и  , то
, то 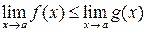 .
.
Теорема 5. («о двух милиционерах») Пусть в некоторой окрестности  для функций
для функций  ,
,  ,
,  имеют место неравенства
имеют место неравенства 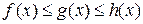 . Если существуют конечные пределы
. Если существуют конечные пределы  , то существует предел
, то существует предел  .
.
Теорема 6. (об арифметических операциях с пределами функций).Если функции  и
и  имеют конечные пределы при
имеют конечные пределы при 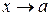 , то справедливы равенства
, то справедливы равенства
 ,
,  ,
,
а если  , то и равенство
, то и равенство
 .
.
Теорема 7. (о замене переменной в пределах). Пусть выполнены три условия:
1) существует конечный предел  ;
;
2) существует конечный предел  ;
;
3) существует такая проколотая окрестность  , что для любого
, что для любого 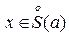 выполнено условие
выполнено условие  .
.
Тогда существует 
Теорема 8. Если существуют конечные пределы  и
и  , то существует предел
, то существует предел  .
.