
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 1.Сравнить бесконечно малые и при .
|
|
Решение. Для того, чтобы сравнить бесконечно малые, необходимо найти предел их отношения:
 .
.
Итак,  является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем  ,
, 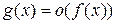 при
при  .
.
Пример 2. Найти предел, используя эквивалентные бесконечно малые функции  .
.
Решение. Имеем неопределенность вида  . Для ее раскрытия воспользуемся теоремой о замене бесконечно малых функций эквивалентными им бесконечно малыми. Так как
. Для ее раскрытия воспользуемся теоремой о замене бесконечно малых функций эквивалентными им бесконечно малыми. Так как  и
и  , то
, то
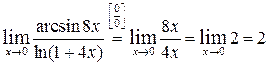 .
.
Задания для самостоятельной работы
n 37. Сравнить бесконечно малые функции.
а)  и и  при при  ; ;
| б)  и и  при при  ; ;
|
в) 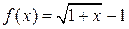 и и  при при  ; ;
| г)  и и  при при  ; ;
|
д) 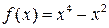 и и  при при  ; ;
| е)  и и  при при  ; ;
|
ж)  и и  при при  ; ;
| з)  и и  при при  ; ;
|
и) 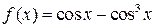 и и 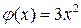 при при  ; ;
| к)  и и  при при  . .
|
n 38. Вычислить пределы, используя принцип замены эквивалентных бесконечно малых функций.
а)  , ,  , ,  , ,  ; ;
| б)  , ,  , ,  , ,  ; ;
|
в)  , ,  , ,  , ,  ; ;
| г)  , ,  , ,  , , 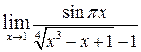 ; ;
|
д) 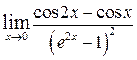 , ,  , ,  , ,  ; ;
| е) 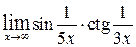 , , 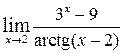 , , 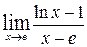 , ,  ; ;
|
ж) 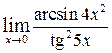 , ,  , , 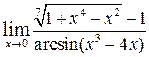 , ,  ; ;
| з)  , ,  , ,  , ,  ; ;
|
и)  , ,  , ,  , , 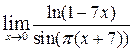 ; ;
| к) 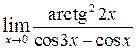 , , 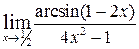 , ,  , ,  . .
|
Задания для самостоятельной работы
n 19. Доказать равенство.
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 20. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  ; ;
|
n 21. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 22. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 23. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е) 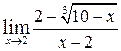 ; ;
|
ж) 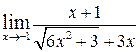 ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 24. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 25. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 26. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 27. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 28. Вычислить
а) 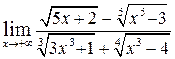 ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д) 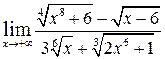 ; ;
| е)  ; ;
|
ж) 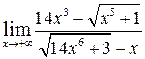 ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 29. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 30. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 31. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 32. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г) 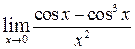 ; ;
|
д)  ; ;
| е)  ; ;
|
ж) 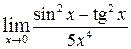 ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 33. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 34. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 35. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к)  . .
|
n 36. Вычислить
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  ; ;
|
д)  ; ;
| е) 
|
ж)  ; ;
| з)  ; ;
|
и)  ; ;
| к) 
|
Задания для самостоятельной работы
n 37. Сравнить бесконечно малые функции.
а)  и и  при при  ; ;
| б)  и и  при при  ; ;
|
в) 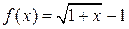 и и  при при  ; ;
| г)  и и  при при  ; ;
|
д) 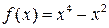 и и  при при  ; ;
| е)  и и  при при  ; ;
|
ж)  и и  при при  ; ;
| з)  и и  при при  ; ;
|
и) 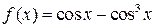 и и 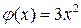 при при  ; ;
| к)  и и  при при  . .
|
n 38. Вычислить пределы, используя принцип замены эквивалентных бесконечно малых функций.
а)  , ,  , ,  , ,  ; ;
| б)  , ,  , ,  , ,  ; ;
|
в)  , ,  , ,  , ,  ; ;
| г)  , ,  , ,  , , 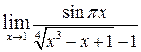 ; ;
|
д) 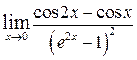 , ,  , ,  , ,  ; ;
| е) 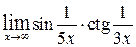 , , 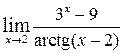 , , 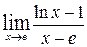 , ,  ; ;
|
ж) 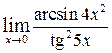 , ,  , , 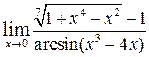 , ,  ; ;
| з)  , ,  , ,  , ,  ; ;
|
и)  , ,  , ,  , , 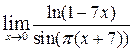 ; ;
| к) 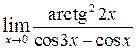 , , 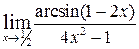 , ,  , ,  . .
|