
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Односторонние пределы
|
|
Понятие предела функции в точке можно разложить на две составляющие части: предел функции  , когда
, когда  , оставаясь меньше
, оставаясь меньше  , т.е.
, т.е.  слева, и предел функции
слева, и предел функции  , когда
, когда  , оставаясь больше
, оставаясь больше  , т.е.
, т.е.  справа. В этом случае говорят об односторонних пределах, обозначая их
справа. В этом случае говорят об односторонних пределах, обозначая их  или
или  (для левостороннего предела) и
(для левостороннего предела) и  или
или  (для правостороннего предела).
(для правостороннего предела).
Определение. Пусть точка  является предельной точкой для множества
является предельной точкой для множества  . Тогда число
. Тогда число  называется пределом слева функции
называется пределом слева функции  при
при  , если
, если
 .
.
Определение. Пусть точка  является предельной точкой для множества
является предельной точкой для множества  . Тогда число
. Тогда число  называется пределом справа функции
называется пределом справа функции  при
при  , если
, если
 .
.
Сравнение этих определений и определения предела функции в точке  показывает, что если функция имеет предел в точке
показывает, что если функция имеет предел в точке  , то этот предел одновременно является ее левосторонним и правосторонним пределами в этой точке.
, то этот предел одновременно является ее левосторонним и правосторонним пределами в этой точке.
Связь между пределом и односторонними пределами функции устанавливает следующая теорема.
Теорема. Для того чтобы существовал  необходимо и достаточно, чтобы существовали односторонние пределы
необходимо и достаточно, чтобы существовали односторонние пределы  и
и  , и
, и  =
=  . В этом случае общее значение односторонних пределов равно значению предела функции:
. В этом случае общее значение односторонних пределов равно значению предела функции:  .
.
Замечание. Предел элементарной функции  при
при 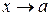 , где
, где  принадлежит области её определения, равен значению функции при
принадлежит области её определения, равен значению функции при  . В этом случае говорят, что функция
. В этом случае говорят, что функция  непрерывна в точке
непрерывна в точке  .
.