Бесконечно малые величины

Определение. Функция называется бесконечно малой (б.м.в.) при (), если .

Основные свойства бесконечно малых величин:

1. функция является б.м.в. при .

2. Сумма, разность и произведение двух б.м.в. при являются б.м.в. при .

3. Если функция является б.м.в. при , а функция ограничена в некоторой окрестности точки , то произведение является б.м.в. при .

Определение. Пусть и – две б.м.в. при и в некоторой окрестности и существует . Тогда:

1. если , то называют бесконечно малой более высокого порядка, чем при , и пишут при (читается: равна «о» малое от );

2. если , то называют бесконечно малой более высокого порядка, чем при , и пишут 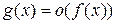при (читается: равна «о» малое от );

3. если (), то и называют бесконечно малыми одного порядка при и пишут при . В частности, если , то и называют эквивалентными бесконечно малыми при и пишут при .

Основные эквивалентности при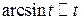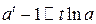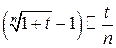