Предел функции, его вычисление.

Изложение первого учебного вопроса следует начать с повторения определения предела функции.

Пусть функция f(x) определена на некотором промежутке Х и пусть точка или .

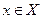Число А называется пределом функции f(x) в точке х=х₀, если для любого числа > 0 существует число > 0 такое, что для всех , х≠ х₀, удовлетворяющих неравенству |х-х₀ |< , выполняется неравенство |f(x)-A|< .

Пример 1.1. Используя определение, доказать, что функция в точке 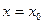имеет предел, равный т.е.

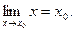
Решение. Возьмем любое Тогда если взять то для всех удовлетворяющих неравенству выполняется требуемое неравенство следовательно,

Пример 1.2. Используя определение, доказать, что функция в точке имеет предел, равный единице, т.е.

Решение. Возьмем любое Задача состоит в том, чтобы по этому найти такое при котором из неравенства 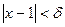следовало бы неравенство Преобразуя последнее неравенство, получаем или Отсюда видно, что если взять то для всех удовлетворяющих неравенству выполняется требуемое неравенство 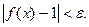Это и означает, что В частности, если то если то и т.д.

Примеры для самостоятельной работы:

1.3. Используя определение, доказать, что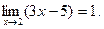

Далее рассмотрим свойства пределов:

Теорема 1. Пусть функции f(x) и g(x) имеют в точке х₀ пределы В и С. Тогда функция f(x)±g(x), f(x)·g(x) и f(x)/g(x) (при С≠ 0) имеют в точке х ₀ пределы, равные соответственно В±С, В·С и В/С, т.е.

Замечание. Теорема 1 верна также и в случае, когда х₀ является одним из символов или .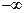

Функция f(x) называется непрерывной в точке х=х₀, если предел функции и ее значение в этой точке равны т. е.

f(x)=f(x₀).

Пример 1.4. Вычислить предел функции

Решение. Так как 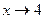, то числитель дроби стремится к числу 5*4+2=22, а знаменатель – к числу 2*4+3=11. Следовательно, на основании теоремы 1 (предел суммы и произведения) имеем

Примеры для самостоятельной работы:

Вычислить пределы функций:

1.5. 1.6. 1.7.

Ответы.

1.5. -8; 1.6. 30; 1.7. 0.

Виды неопределенностей и методы их раскрытия.

Виды неопределенностей и методы их раскрытия целесообразно пояснить непосредственно на примерах.

Пример 2.1. Вычислить предел функции

Решение. Числитель и знаменатель дроби неограниченно возрастают при . В таком случае говорят, что имеет место неопределенность вида . Разделив на х числитель и знаменатель дроби, получаем

так как при каждая из дробей 5/ x и 7/ x стремится к нулю.

Пример 2.2. Найти предел функции .

Решение. Полагая , , имеем , , т.е. как говорят, имеет место неопределённость вида . Пользоваться теоремой о пределе частного нельзя. Для раскрытия неопределённости поступаем так. В определении предела функции в точке сама точка из рассмотрения исключается. Заметив это, представим данную функцию в виде

откуда, сокращая на , получим

Поэтому

.

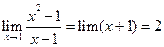Пример 2.3. Найти

Решение. Имеем неопределенность вида 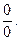Непосредственно теорему 1 (предел частного) применить нельзя. Необходимо, как говорят, раскрыть эту неопределенность. Для этого разложим числитель на множители и сократим на общий множитель который обращает в нуль знаменатель и числитель дроби. Получаем

Так как знаменатель теперь не равен нулю, то неопределенность раскрыта. Применяя теорему о пределе частного, окончательно находим

Пример 2.4. Найти

Решение. Имеем неопределенность вида Разделив на числитель и знаменатель дроби, а затем применив теорему 1, получим

Пример 2.5. Найти предел

Решение. Непосредственная подстановка предельного значения аргумента х =2 приводит к неопределенности вида . Чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и сократим члены дроби на общий множитель (х-2). Так как аргумент х только стремится к своему предельному значению 2, но не совпадает с ним, то множитель (х-2) отличен от нуля при х®2:

Пример 2.6.

Решение. Здесь числитель и знаменатель дроби при 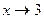стремятся к нулю (неопределенность вида ). Имеем

если 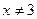, то 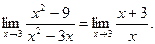Но при 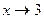дробь стремится к числу . Итак,

Пример 2.7. Найти

Решение. Здесь имеет место неопределенность вида 0/0. Разложим на множители числитель и знаменатель дроби:

Пример 2.8.

Решение. Это – также неопределенность вида 0/0. Имеем

Пример 2.9. Найти

Решение. Пределы числителя и знаменателя в точке х =0 равны нулю, т.е. опять имеем неопределённость вида . Для её раскрытия умножим числитель и знаменатель данной дроби на . При 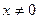имеем

К полученной функции применима теорема о пределе частного, так что

.

Применение замечательных пределов.

При нахождении пределов используются также следующие пределы:

(первый замечательный предел);

(второй замечательный предел).

Пример 3.1. Вычислить предел

Решение. Пусть arctg 2x=y. Тогда 2х=tg y; очевидно, что если х®0, то y®0. Следовательно,

(используем первый замечательный предел).

Искомый предел можно найти иначе. Известно, что при нахождении предела отношения двух бесконечно малых величин можно каждую из них (или только одну) заменить другой бесконечно малой, ей эквивалентной. Так как при х®0 arctg 2x~2х, то

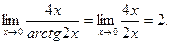
Пример 3.2. Вычислить предел .

Решение. При х®¥ основание стремится к 1, а показатель степени 4х+1 стремиться к бесконечности. Следовательно, имеем неопределенность вида 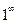. Представим основание в виде суммы 1 и некоторой бесконечно малой величины:

Тогда

Положим 2х+3=-4у; при х®+¥ переменная у® -¥. Выразим показатель степени через новую переменную у. Так как 2х=-4у-3, то 4х+1=-8у-5. Таким образом,

(используем второй замечательный предел).

Пример 3.3. Вычислить предел .

Решение. Имеем

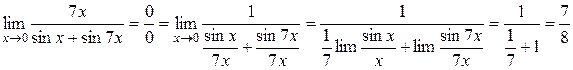
(использовали первый замечательный предел).

Пример 3.4. Найти предел .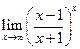

Решение.

(использовали второй замечательный предел).

Задачи для самостоятельного решения.

Найти пределы:

3.5. Ответ. .

3.6. Ответ. .