
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 2.4.
|
|
Вычислить производную сложной функции 
Решение.
Производная показательной функции находится по правилу
 .
.
Показатель в свою очередь тоже является степенной функцией переменной x.
По правилу дифференцирования сложной функции получаем:

Пример 2.5.
Вычислить производную сложной функции 
Решение.
 , u = x2 Þ
, u = x2 Þ  ,
,  Þ
Þ 
Пример 2.6.
Вычислить производную сложной функции 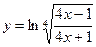
Решение.
Предварительно, пользуясь правилом логарифмирования корня и дроби, преобразуем правую часть:

Далее, применяя правила и формулы дифференцирования, получим:

Примеры для самостоятельной работы:
Вычислить производные функций:
2.7. 
2.8. 
2.9. 
2.10. 
Ответы:
2.7.  2.8.
2.8.  2.9.
2.9.  2.10.
2.10. 
ВОПРОСЫ для подготовки к зачету и экзамену по ЛА 1курс ЭФ Заочное отделение.
1. Матрицы. Типы матриц. Обратная матрица.
2. Матрицы. Действия с матрицами
3. Определители квадратных матриц и их свойства
4. Минор и алгебраическое дополнение элемента определителя. Разложение определителя по элементам какого-либо ряда.
5. Решение системы линейных уравнений по формулам Крамера.
6. Решение системы линейных уравнений с помощью обратной матрицы.
7. n -мерный вектор. Линейное пространство. Базис и размерность линейного пространства. Координаты вектора.
8. Линейная независимость векторов. Признак линейной независимости векторов.
9. Ранг матрицы.
10. Метод Гаусса решения систем линейных уравнений.
Вопросы к экз. по МА
11. Переменные и их пределы. Величины бесконечно малые и бесконечно большие.
12. Теоремы о пределах последовательностей. Раскрытие некоторых типов
неопределенностей. Замечательные пределы.
13. Функции одной переменной. Классификации функций.
14. Предел функции в точке. Предел функции на бесконечности.
15. Односторонние пределы функции.
16. Сравнение функций. Эквивалентные бесконечно малые функции.
17. Определение 1 и определение 2 непрерывности функции в точке. Классификация точек разрыва.
18. Производная функции в точке, ее физический и геометрический смысл.
19. Производная суммы, разности, произведения и частного.
20. Сложная; неявная функции. Правило дифференцирования сложной; неявной функций.
21. Дифференциал функции и его геометрический смысл.
22. Условие монотонности функции.
23. Экстремум функции. Теорема Ферма (необходимое условие экстремумов).
24. Достаточные условия экстремумов.
25. Направление вогнутости графика функции (аналитический признак).
26. Точки перегиба и выпрямления (необходимые условия, достаточные условия).
27. Приложения производных. Правило Лопиталя.