Правила дифференцирования. Производная сложной и обратной функции.

Если функции и = u(x) и v = v(x) дифференцируемы в точке х, то сумма, разность, произведение и частное этих функций (частное при условии, что v(x) ¹ 0) также дифференцируемы в этой точке и имеют место следующие формулы:

1) 2) 3)

4) Производная постоянной равна 0:

если , где , то .

5) Постоянный множитель можно выносить за знак производной:

Если где , то .

Замечание. Если имеем функцию вида: , где , то .

Производная сложной функции.

Пусть и , тогда — сложная функция с промежуточным аргументом и и независимым аргументом х.

Теорема. Если функция имеет в некоторой точке х производную , а функция имеет производную в соответствующей точке , то сложная функция в точке х также имеет производную, которая равна:

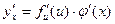или .

То есть производная сложной функции равна произведению производной данной функции по промежуточному аргументу и на производную промежуточного аргумента по х. Это правило остается в силе, если промежуточных аргументов несколько. Так, если , , , то .

Пример 1. Дана функция . Найти .

Решение. Функцию представим как . Применяя формулу для производной сложной функции, получаем

.

Подставляя вместо и его выражение окончательно получаем:

.

Производная обратной функции.

Пусть дана функция строго монотонная (т.е. возрастающая или убывающая), определенная на некотором интервале. Рассматривая значения y как значения аргумента, а значения х как значения функции, получаем х как функцию y: Эта функция называется обратной для функции .

Теорема. Если функция строго монотонна на некотором интервале и имеет неравную нулю производную в произвольной точке этого интервала, то обратная ей функция также имеет производную 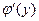в соответствующей точке, определяемую равенством или .

Таким образом, производная одной из двух взаимно-обратных функций равна обратной величине производной второй из этих функций ).

Пример 2. Дано . Найти .

Решение. Обратная функция

.

.

Следовательно .

Аналогично находятся производные обратных тригонометрических функций:

1.

2.

3.

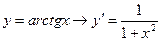
4.

Таблица производных основных элементарных функций.

При изучении первого учебного вопроса необходимо предварительно напомнить обучающимся изложенные на лекции понятия производной (наиболее сильных курсантов можно вызвать к доске).

Производной функции в точке называется предел при отношения приращения функции в этой точке к приращению аргумента (при условии, что этот предел существует).

Производная обозначается или

Итак, по определению,

(1)

Нахождение производной называется дифференцированием функции.

Пример 1.1. Используя определение производной, найти производную функции в точке

Решение. Придавая аргументу в точке приращение найдем соответствующее приращение функции:

Составим отношение

Найдем предел этого отношения при

Следовательно, производная функции в точке равна числу 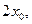что в принятых обозначениях можно записать так: .

Однако, рассмотренный в данном примере метод вычисления производных является громоздким, и на практике для дифференцирования функций используются готовые табличные формулы, полученные на основании соотношения (1). Это формулы производных простейших элементарных функций.

Очень важно обратить внимание обучающихся на необходимость знания наизусть нижеследующей таблицы производных основных элементарных функций.

Таблица производных основных элементарных функций.

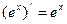
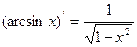
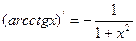
Пример 1.2. Вычислить производную функции .

Решение.

– это степенная функция. По таблице производных используем формулу для производной степенной функции

Применяя указанную формулу к функции , находим

Пример 1.3. Вычислить производную функции .

Решение. – это показательная функция. Используя таблицу производных, находим производную данной показательной функции:

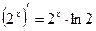
Примеры для самостоятельной работы (решаются под руководством преподавателя):

Вычислить производные элементарных функций:

1.4. ; 1.5. ; 1.6.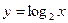

Ответы:

1.4. ; 1.5. ; 1.6. 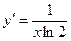.