Типовой пример

Вычислить приближенно.

1)

► Имеем . Тогда .◄

2) ln 0, 95.

► . Применена формула .◄

3) cos 0, 1.

► . Применена формула .◄

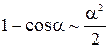§4. Непрерывность функции

Непрерывность функции в точке

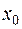Пусть функция определена в точке и в некоторой окрестности точки .

Функция называется непрерывной в точке , если предел её в этой точке равен значению функции в этой точке, т.е. если

= . (1)

Следствие. Если функция непрерывна в точке , то к пределу можно перейти под знаком функции, т.е.

= . (2)

Функция называется непрерывной в точке 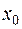, если выполняется условие .

Разность – = называют приращением аргумента, а разность – = 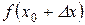– = – приращением функции в точке = .

Функция называется непрерывной в точке 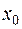, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, т.е. .