
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Типовые примеры
|
|
1)  .
.
► Если необходимо найти предел  , можно предварительно привести к общему знаменателю
, можно предварительно привести к общему знаменателю
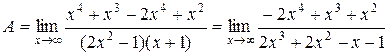 .
.
Поделив на член, имеющий максимальную степень, получим в числителе постоянную величину, а в знаменателе – все члены, стремящиеся к 0, то есть
 .◄
.◄
2) 
► Данный пример решается аналогично предыдущему:
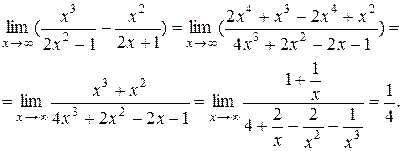 ◄
◄
3)  .
.
► При подстановке  , получим
, получим  .◄
.◄
4)  .
.
► В этом пределе, если подставить  , то получится неопределенность, которую можно преодолеть, если разложить разность кубов в знаменателе
, то получится неопределенность, которую можно преодолеть, если разложить разность кубов в знаменателе  , а числитель в виде:
, а числитель в виде: 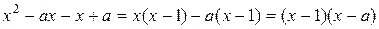 .
.
Тогда  и подставив
и подставив  , получим:
, получим:  .◄
.◄
5)  .
.
► Если необходимо найти предел рациональной функции  , то при делении на член с минимальной степенью, получим
, то при делении на член с минимальной степенью, получим  ; и, устремив
; и, устремив  к 0, получим:
к 0, получим:  .◄
.◄
6)  ► Имеет место неопределенность вида
► Имеет место неопределенность вида 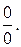 Так как
Так как  является корнем многочленов из числителя и знаменателя, то
является корнем многочленов из числителя и знаменателя, то  выделяется как сомножитель в числителе и знаменателе. Для разложения на множители выполним деление «уголком» Имеем
выделяется как сомножитель в числителе и знаменателе. Для разложения на множители выполним деление «уголком» Имеем
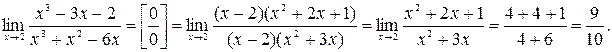 ◄
◄
Если в пределах содержатся иррациональные выражения, то приходится вводить новые переменные для получения рационального выражения, или же переводить иррациональности из знаменателя в числитель и наоборот.
7)  .
.
► Сделаем замену переменной. Заменим  , при
, при 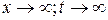 , получим
, получим  .◄
.◄
8) 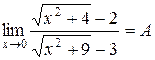 .
.
► Если числитель и знаменатель умножить на одно и то же число, то предел не изменится. Умножим числитель на  и разделим на это же выражение, чтобы предел не изменился, а знаменатель умножим на
и разделим на это же выражение, чтобы предел не изменился, а знаменатель умножим на  и разделим, на это же выражение. Тогда получим:
и разделим, на это же выражение. Тогда получим:
 ◄
◄
9) 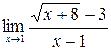 .
.
►  [
[  ]=(Умножим числитель и знаменатель на выражение, сопряженное числителю) =
]=(Умножим числитель и знаменатель на выражение, сопряженное числителю) =
 ◄
◄
10) 
► Имеет место неопределенность вида 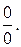 Произведем замену
Произведем замену 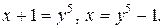 Тогда при
Тогда при 
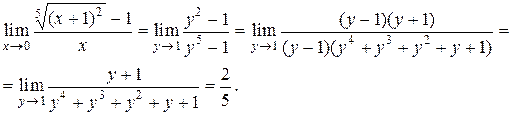 ◄
◄
11) 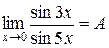 .
.
► Для вычисления такого предела сведем его к 1-му замечательному пределу. Для этого умножим и разделим числитель на  , а знаменатель на
, а знаменатель на  , тогда
, тогда  .◄
.◄
12) 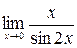 .
.
►  = [ по первому замечательному пределу ] =
= [ по первому замечательному пределу ] =  ◄
◄
13)  .
.
► 
◄
14)  .
.
► Для вычисления этого предела сведем его ко второму замечательному пределу. С этой целью из рационального выражения в скобках выделим целую часть и представим ее в виде правильной дроби. Так поступают в тех случаях, когда  , где
, где  , а
, а  , где
, где  ;
;
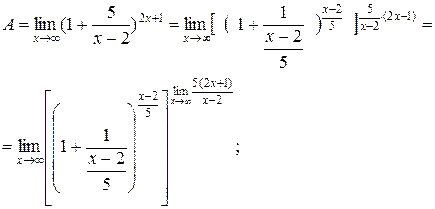
 , а
, а  , то окончательно
, то окончательно 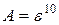 . Здесь использовалась непрерывность композиции непрерывных функций. ◄
. Здесь использовалась непрерывность композиции непрерывных функций. ◄
15) ►  =[ по второму замечательному пределу ] =
=[ по второму замечательному пределу ] =
 ◄
◄
16) 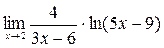 .
.
► 
◄
17)  .
.
► Имеем  и
и  . Поэтому
. Поэтому  .◄
.◄
18) Найдите  и
и  , если
, если  .
.
► Рассмотрим нахождения левого и правого пределов. Пусть  Если
Если  Следовательно,
Следовательно,  Если же
Если же 
 и
и 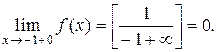
Таким образом,  Это означает, что не существует
Это означает, что не существует  ◄
◄