
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
|
|
Предел функции
К элементарным функциям относятся: 1) простейшие элементарные функции: постоянная с, степенная  , показательная
, показательная  , логарифмическая
, логарифмическая  , тригонометрическая
, тригонометрическая  , обратные тригонометрические
, обратные тригонометрические  ; 2) все функции, получающиеся из простейших элементарных функций путем применения конечного числа следующих четырех операций: сложение, умножение, деление, суперпозиция функций (сложная функция). В класс элементарных функций попадают: а) многочлен; б) рациональная дробь (отношение двух многочленов); в)
; 2) все функции, получающиеся из простейших элементарных функций путем применения конечного числа следующих четырех операций: сложение, умножение, деление, суперпозиция функций (сложная функция). В класс элементарных функций попадают: а) многочлен; б) рациональная дробь (отношение двух многочленов); в)  , т.к.
, т.к.  ; г)
; г)  ; д)
; д)  , т.к.
, т.к.  , и множество других.
, и множество других.
Пусть функция  определена во всех точках интервала
определена во всех точках интервала  , за исключением, быть может, точки
, за исключением, быть может, точки  . Число А называется пределом функции
. Число А называется пределом функции  в точке
в точке  , если для любого
, если для любого  существует число
существует число  такое, что для любого x, удовлетворяющего неравенству
такое, что для любого x, удовлетворяющего неравенству  , выполняется неравенство
, выполняется неравенство  , при этом пишут
, при этом пишут  . Можно дать другое, равносильное приведенному, определение: число A называется пределом функции
. Можно дать другое, равносильное приведенному, определение: число A называется пределом функции  в точке x0, если для любой последовательности чисел
в точке x0, если для любой последовательности чисел  , сходящейся к
, сходящейся к  ,
, 
 . Если
. Если  определена в интервале
определена в интервале  , то число A называется пределом
, то число A называется пределом  при
при 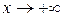 , если для любого
, если для любого  существует число
существует число  , такое, что неравенство
, такое, что неравенство  влечет за собой неравенство
влечет за собой неравенство  . При этом пишут
. При этом пишут  или
или  . Аналогично определяется
. Аналогично определяется  .
.
Данная страница нарушает авторские права?