
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Типовые примеры. Найти пределы функций.
|
|
Найти пределы функций.
1)  .
.
► 
 . Здесь при
. Здесь при  и поэтому применяем формулу из группы (2)
и поэтому применяем формулу из группы (2) 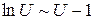 . Так как
. Так как  , то применяем формулы
, то применяем формулы  и
и  .◄
.◄
2)  .
.
► 
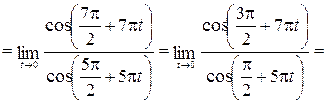
 .◄
.◄
3)  .
.
► 
 .Здесь применены формулы
.Здесь применены формулы  .◄
.◄
4)  .
.
►  ◄
◄
5) 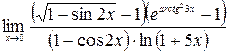 .
.
►  . Имеем
. Имеем
 ,
,
 ,
,  ,
,  . Учитывая это, получаем
. Учитывая это, получаем
 =
=  .◄
.◄
6)  .
.
► Имеем  ~
~  =
=  ,
,  ~
~  . Отсюда находим
. Отсюда находим  =
=  =
=  =
=
= 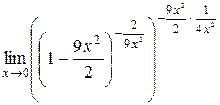 =
=  =
=  .◄
.◄
Следует помнить, что принцип эквивалентности не всегда можно применять. Это прежде всего касается случая, когда эквивалентность применяют к сумме. Так, если при  применять эквивалентность к выражению tg x -sin x, то получите не переменную, а 0. По этой же причине нельзя применять эквивалентность при
применять эквивалентность к выражению tg x -sin x, то получите не переменную, а 0. По этой же причине нельзя применять эквивалентность при  в выражениях
в выражениях  ,
,  . Как быть в таком случае? Надо данные выражения путем элементарных преобразований привести к виду, где можно применить эквивалентность.
. Как быть в таком случае? Надо данные выражения путем элементарных преобразований привести к виду, где можно применить эквивалентность.
Отметим, что все формулы эквивалентности можно использовать для приближенных вычислений.