Типовой пример. Доказать, пользуясь определением предела последовательности, что .

Доказать, пользуясь определением предела последовательности, что .

► Имеем:

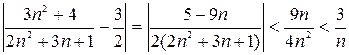. Решив неравенство , получим 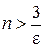и ясно, что достаточно выбрать 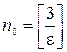, чтобы для 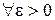неравенство выполнялось для всех . Что и требовалось.

Типовой пример

Дана последовательность 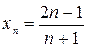. Найдите: 1) ; 2) такое, что для всех выполняется неравенство .

1) ► Имеем

.

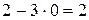2) ► Найдём требуемое . Из проделанных выше выкладок следует, что должно быть подобрано так, чтобы для всех

или 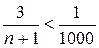; отсюда следует , . Следовательно, можно взять .

Предел отношения многочленов

Пусть x _n и y _n многочлены от n степени k и m соответственно, т.е.

x _n= P _k(n)= a ₀ n ^k+ a ₁ n ^k-1+...+ a _k, y _n= Q _m(n)= b ₀ n ^m+ b ₁ n ^m-1+...+ b _m

Докажем, что предел отношения многочленов равен пределу отношения их старших членов, т.е.

.

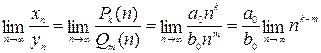Имеем: , что и требовалось.

Итак,