
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные элементарные функции и их графики
|
|
Основными элементарными функциями называют следующие функции.
1. Степенная функция  ,
,  .
.
Примеры графиков степенных функций, соответствующих различным показателям степени, показаны на рисунках.
 2. Показательная функция
2. Показательная функция  ,
,  ,
,  .
.
На рисунке показаны графики функций, соответствующие различным основаниям.
3. Логарифмическая функция  ,
,  ,
,  .
.
 Графики логарифмических функций, соответствующие различным основаниям логарифма, показаны на рисунке.
Графики логарифмических функций, соответствующие различным основаниям логарифма, показаны на рисунке.
4. Тригонометрические функции  ,
,  ,
,  ,
,  .
.
Графики тригонометрических функций показаны на рисунках.




5. Обратные тригонометрические функции  ,
,  ,
,  ,
,  .
.
Графики обратных тригонометрических функций показаны на рисунках
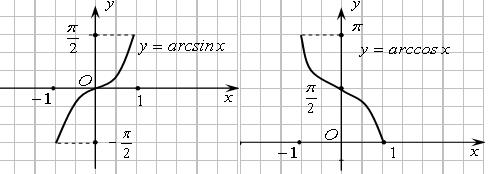

Все функции, получаемые из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными функциями.
Пример
Функции  ,
,  ,
,  – элементарные; функция
– элементарные; функция  не является элементарной. В качестве примера неэлементарной функции укажем модуль действительного числа x
не является элементарной. В качестве примера неэлементарной функции укажем модуль действительного числа x

Напомним, что графиком функции 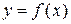 называется множество точек плоскости с координатами (x,
называется множество точек плоскости с координатами (x,  ), где
), где  . Из определения функции следует, что график функции
. Из определения функции следует, что график функции 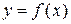 имеет ровно одну точку пересечения с вертикальной прямой x = a для любого элемента
имеет ровно одну точку пересечения с вертикальной прямой x = a для любого элемента  На рис. (а) изображен график функции y =| x |, а на рис. (б) - пример кривой L, не являющейся графиком никакой функции.
На рис. (а) изображен график функции y =| x |, а на рис. (б) - пример кривой L, не являющейся графиком никакой функции.

| 
|
| а | б |