Типовой пример. Докажите, что функция строго убывает, если .

Докажите, что функция строго убывает, если .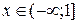

► Функция строго убывает на , если для любых значений и из этого полуинтервала таких, что , следует, что .

Рассмотрим разность:

так какпри и, кроме того, выполнены условия ; в силу . Итак, мы доказали, что для любых значений аргументов из промежутка , из условия , следует, что т.е. функция строго убывает на .◄

Функция , определенная на множестве , называется периодической на этом множестве с периодом , где – положительное число, если выполняются условия: и . Если – период, то периодом функции также будут числа , где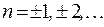

Пример

Для функции периодами будут числа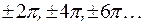

Функция , определенная на множестве , называется ограниченной на этом множестве, если существует такое число , что для всех выполняется неравенство 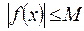. Коротко можно

записать так:

.

График ограниченной функции расположен между прямым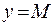и и . Например, функция ограничена, так как .