
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные характеристики функции
|
|
Функция  , определенная на множестве
, определенная на множестве  , область определения которой симметрична относительно начала координат, называется: четной, если
, область определения которой симметрична относительно начала координат, называется: четной, если  выполняются условия
выполняются условия 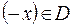 и
и  ; нечетной, если
; нечетной, если  выполняются условия
выполняются условия 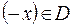 и
и  . В противном случае функция
. В противном случае функция  называется функцией общего вида.
называется функцией общего вида.
График четной функции симметричен относительно оси  , график нечетной функции симметричен относительно начала координат.
, график нечетной функции симметричен относительно начала координат.
Например, функция  - четная, а функция
- четная, а функция  –функция общего вида.
–функция общего вида.
Пусть функция  определена на множестве
определена на множестве  , интервал
, интервал  .
.
Если для любых  и
и  из интервала
из интервала  , причем
, причем  , выполняется неравенство:
, выполняется неравенство:
1)  , то функция
, то функция  называется неубывающей на
называется неубывающей на  ;
;
2)  , то функция
, то функция  называется невозрастающей на
называется невозрастающей на  ;
;
3)  , то функция
, то функция  называется возрастающей на
называется возрастающей на  ;
;
4)  , то функция
, то функция  называется убывающей на
называется убывающей на  .
.
 Во всех рассмотренных случаях функции называются монотонными, авозрастающая и убывающая функции строго монотонными.
Во всех рассмотренных случаях функции называются монотонными, авозрастающая и убывающая функции строго монотонными.
Пример
На рисунке функция  на
на  строго монотонная; на
строго монотонная; на  монотонная.◄
монотонная.◄