
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Числовые множества. Комплексные числа
|
|
Множества, элементами которых являются числа, называются числовыми множествами.
Например:
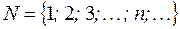 – множество натуральных чисел;
– множество натуральных чисел;
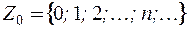 – множество целых неотрицательных чисел;
– множество целых неотрицательных чисел;
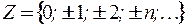 – множество целых чисел;
– множество целых чисел;
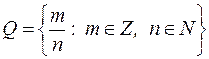 – множество рациональных чисел;
– множество рациональных чисел;
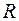 – множество действительных чисел.
– множество действительных чисел.
Между этими множествами существует соотношение 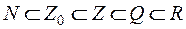 .
.
Множество 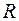 содержит рациональные и иррациональные числа. Всякое рациональное число выражается дробью. Например,
содержит рациональные и иррациональные числа. Всякое рациональное число выражается дробью. Например, 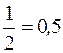 – (конечная десятичная дробь);
– (конечная десятичная дробь); 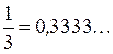 – (бесконечная периодическая дробь). Действительные числа, не являющиеся рациональными, называются иррациональными числами. Это бесконечные непериодические дроби. Например,
– (бесконечная периодическая дробь). Действительные числа, не являющиеся рациональными, называются иррациональными числами. Это бесконечные непериодические дроби. Например, 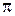 ,
, 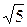 .
.
Рассмотрим, так называемые, комплексные числа, которые возникают уже при решении, например, уравнения 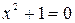 .
.
Комплексным числом называется выражение вида 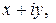 i- символ, называемый мнимой единицей и обладающий свойством
i- символ, называемый мнимой единицей и обладающий свойством  . Действительные числа x и y называются действительной и мнимой частями комплексного числа
. Действительные числа x и y называются действительной и мнимой частями комплексного числа 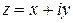 и обозначаются через Re z и Im z соответственно.
и обозначаются через Re z и Im z соответственно.
Всякое комплексное число 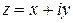 может быть изображено точкой
может быть изображено точкой 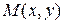 с абсциссой x и ординатой y в координатной плоскости, называемой комплексной.
с абсциссой x и ординатой y в координатной плоскости, называемой комплексной.
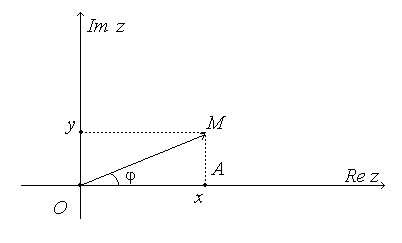
Заметим, что любое вещественное число является комплексным, мнимая часть которого равна 0. На комплексной плоскости вещественным числам соответствуют точки, лежащие на оси Ox.
Число 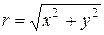 называется модулем комплексного числа
называется модулем комплексного числа 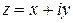 , обозначается символом | z | и равно расстоянию от начала координат О до точки M, изображающей число z.
, обозначается символом | z | и равно расстоянию от начала координат О до точки M, изображающей число z.
Угол 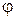 между положительным направлением оси Оx и вектором
между положительным направлением оси Оx и вектором 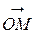 называется аргументом Arg z комплексного числа
называется аргументом Arg z комплексного числа 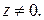 При этом
При этом 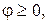 если движение от оси Ox осуществляется против часовой стрелки, и
если движение от оси Ox осуществляется против часовой стрелки, и 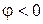 с противном случае. Значения Arg z определяется неоднозначно, с точностью до слагаемых, кратных
с противном случае. Значения Arg z определяется неоднозначно, с точностью до слагаемых, кратных 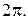 Поэтому из всех значений Arg z выбирается главное значение, которое лежит в интервале
Поэтому из всех значений Arg z выбирается главное значение, которое лежит в интервале 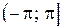 и обозначается через
и обозначается через 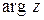 .
.
Главное значение arg z вычисляется по формуле
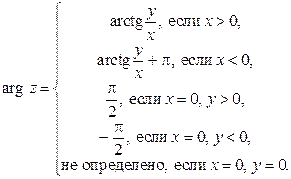
Пример
Для числа 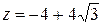 имеем
имеем 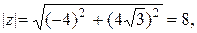
arg z = 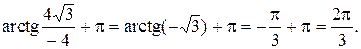
Запись 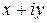 называется алгебраической формой числа z. Из прямоугольного треугольника OAM (см. рис. 1) получаем
называется алгебраической формой числа z. Из прямоугольного треугольника OAM (см. рис. 1) получаем 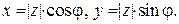 Таким образом, справедливо равенство
Таким образом, справедливо равенство
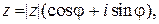
представляющее тригонометрическую форму числа z. Обозначив символом 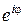 выражение
выражение 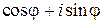 , получаем показательную форму комплексного числа z
, получаем показательную форму комплексного числа z
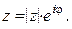

Пример
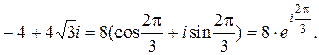
Для числа 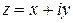 число
число 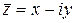 называется сопряженным, а число
называется сопряженным, а число 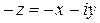 - противоположным.
- противоположным.
Операция сложения комплексных чисел 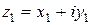 и
и 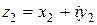 определяется равенством
определяется равенством
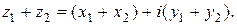
Произведение чисел z 1 и z 2 вычисляется по обычным законам умножения двучленов с учетом соотношения 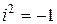 .
.
Например, 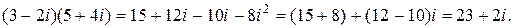
Деление числа z 1 на z 2 происходит по следующему правилу:
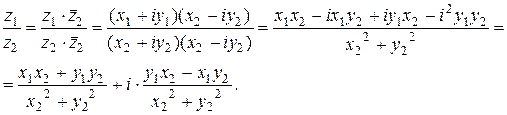
Пример 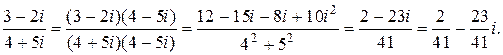
Нетрудно проверить, что при умножении комплексных чисел z 1 и z 2 их модули перемножаются, а аргументы складываются
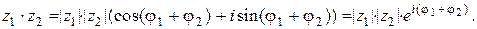
При делении комплексных чисел наоборот происходит деление модулей и вычитание аргументов.
Из формулы умножения следует формула Муавра, позволяющая возводить комплексное число 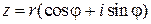 в любую натуральную степень
в любую натуральную степень
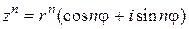 ,
,
или в показательной форме
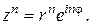
Пусть 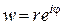 - ненулевое комплексное число. Тогда уравнение
- ненулевое комплексное число. Тогда уравнение 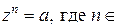 N, имеет ровно n различных решений
N, имеет ровно n различных решений 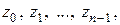 которые можно вычислить по формуле
которые можно вычислить по формуле
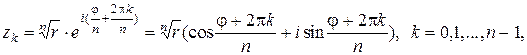
считая 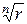 положительным действительным числом, равным арифметическому корню n -й степени из положительного числа r. Числа
положительным действительным числом, равным арифметическому корню n -й степени из положительного числа r. Числа 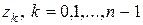 , называются корнями n-й степени из комплексного числа w и обозначаются символом
, называются корнями n-й степени из комплексного числа w и обозначаются символом 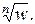 Из записи чисел zk видно, что соответствующие им точки на комплексной плоскости лежат на окружности радиуса
Из записи чисел zk видно, что соответствующие им точки на комплексной плоскости лежат на окружности радиуса 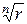 и образуют правильный n - угольник.
и образуют правильный n - угольник.