
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функции действительной переменной
|
|
1. Отображение
Мы говорим, что задано отображение 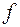 множества
множества  во множество
во множество 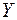 , и пишем
, и пишем  , если каждому элементу
, если каждому элементу  из области определения
из области определения  сопоставлен однозначно определенный элемент
сопоставлен однозначно определенный элемент 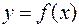 из области действия
из области действия 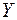 , называемый образом элемента
, называемый образом элемента  при отображении
при отображении 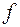 (такое сопоставление символически принято обозначать так:
(такое сопоставление символически принято обозначать так: 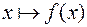 ). При этом не исключается возможность, что одному элементу
). При этом не исключается возможность, что одному элементу  отвечает при отображении
отвечает при отображении 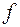 несколько элементов
несколько элементов  , таких, что
, таких, что  . Подмножество
. Подмножество  всех таких элементов называется прообразом элемента
всех таких элементов называется прообразом элемента  при отображении
при отображении 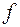 и обозначается
и обозначается  , т.е.
, т.е.  .
.
Более общо, образом множества  при отображении
при отображении 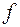 называется множество
называется множество  . Прообразом множества
. Прообразом множества  при отображении
при отображении 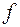 (обозначают:
(обозначают:  ) называется объединение прообразов всех элементов, входящих в
) называется объединение прообразов всех элементов, входящих в  , т.е.
, т.е.
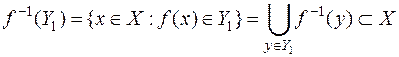 .
.
Отображение 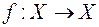 называют также преобразованием множества
называют также преобразованием множества  (в себя). Вместо термина «отображение» часто употребляют термин «оператор» (особенно в функциональном анализе и линейной алгебре). а также «функция» (особенно в случае, когда
(в себя). Вместо термина «отображение» часто употребляют термин «оператор» (особенно в функциональном анализе и линейной алгебре). а также «функция» (особенно в случае, когда 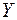 – числовое множество).
– числовое множество).
Переменную 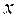 называют аргументом или независимой переменной, а переменную
называют аргументом или независимой переменной, а переменную  – зависимой переменной от х; множество
– зависимой переменной от х; множество 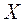 – областью определения функции
– областью определения функции  , а множество
, а множество  – множеством значений функции
– множеством значений функции  ,
,  – закон соответствия.
– закон соответствия.  – множество значений аргумента, при которых формула
– множество значений аргумента, при которых формула  имеет смысл.
имеет смысл.
Кроме буквы  для обозначения функций используют и другие буквы греческого и латинского алфавитов:
для обозначения функций используют и другие буквы греческого и латинского алфавитов:  ,
,  ,
,  ,
,  и так далее.
и так далее.
