
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Множества и операции над ними
|
|
ГЛАВА I. ФУНКЦИИ. ПРЕДЕЛЫ.
НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
Числовые множества
Множества и операции над ними
Под м ножеством понимаем совокупность, систему, семейство некоторых объектов, объединенных по какому-либо признаку. Например, множество студентов университета, множество товаров и услуг, бюджетное множество, множество производственных возможностей, множество ресурсов производства, множество действительных чисел, множество натуральных чисел, множество точек прямой, множество точек на плоскости, множество векторов, множество функций, множество функций одной переменной, множество точек пространства, множество решений квадратного уравнения, и т. д.
Обозначаются множества заглавными буквами латинского алфавита:  . Объекты, из которых состоит множество, называются элементами множества. Элементы множества обозначаются соответственно строчными буквами латинского алфавита:
. Объекты, из которых состоит множество, называются элементами множества. Элементы множества обозначаются соответственно строчными буквами латинского алфавита:  . Например,
. Например, 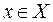 – элемент
– элемент  принадлежит множеству
принадлежит множеству  ;
;  –элемент
–элемент  не принадлежит множеству
не принадлежит множеству  .
.
Будем считать, что мы выбрали и зафиксировали достаточно широкое множество, за пределы которого не будем выходить. Элементы всех множеств, которые мы будем рассматривать, одновременно являются элементами этого широкого фиксированного множества, называемого универсальным множеством (для этого множества будем применять обозначение  ).
).
Множество, не имеющее ни одного элемента, называется пустым множеством. Пустое множество обозначается так:  . Примерами пустых множеств являются: множество треугольников, длины сторон которых равны 2см, 3 см, 7 см; множество рациональных чисел, квадрат которых равен 2; множество решений системы уравнений
. Примерами пустых множеств являются: множество треугольников, длины сторон которых равны 2см, 3 см, 7 см; множество рациональных чисел, квадрат которых равен 2; множество решений системы уравнений  ,
, 
Элементы множества записываются в фигурных скобках, в которых они перечислены или в скобках может быть указано свойство, которым обладают все элементы данного множества:  .
.
Пример
 – множество
– множество  состоит из трех чисел 1, 8, 6;
состоит из трех чисел 1, 8, 6;  – множество
– множество  состоит из всех действительных чисел, удовлетворяющих неравенству
состоит из всех действительных чисел, удовлетворяющих неравенству  .
.
Множество  называется подмножеством множества
называется подмножеством множества  , если каждый элемент множества
, если каждый элемент множества  является элементом множества
является элементом множества  . Обозначается подмножество так:
. Обозначается подмножество так:  (
( включено в
включено в  ) или
) или  (множество
(множество  включает в себя множество
включает в себя множество  ). Знаки
). Знаки  и
и  также называют знаками включения.
также называют знаками включения.
Множества, состоящие из одних и тех же элементов, называются равными множествами. Если  и
и  , то
, то  , следовательно, говорят, что множества
, следовательно, говорят, что множества  и
и  равны или совпадают. Принято считать, что пустое множество принадлежит в качестве подмножества любому множеству; очевидно, также
равны или совпадают. Принято считать, что пустое множество принадлежит в качестве подмножества любому множеству; очевидно, также 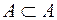 .
. 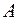 и
и  называют несобственными подмножествами множества
называют несобственными подмножествами множества 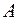 , все остальные подмножества множества
, все остальные подмножества множества 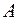 называют собственными.
называют собственными.
Объединением (или суммой) множеств  и
и  называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному их этих множеств. Записывают
называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному их этих множеств. Записывают  или
или  .
.
 |
Понятие объединения обобщается на случай бесконечного числа множеств. Если даны множества
 , то символическая запись
, то символическая запись

означает объединение данных множеств, т.е. множество, каждый элемент которого принадлежит хотя бы одному из данных множеств.
Пример
Объединение множества положительных четных чисел и множества положительных нечетных чисел есть множество натуральных чисел.
Пример
 .
.
Пересечением (или произведением) множеств  и
и  называется множество, состоящее из элементов, каждый из которых одновременно принадлежит множеству
называется множество, состоящее из элементов, каждый из которых одновременно принадлежит множеству  и множеству
и множеству  . Записывают
. Записывают  или
или  .
.
Для бесконечного набора множеств  символ
символ
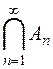
 |
обозначает их пересечение, т.е. множество, каждый элемент которого принадлежит всем данным множествам.
Пример
 .
.
Разностью множеств  и
и  называется совокупность тех элементов
называется совокупность тех элементов  , которые не содержатся в
, которые не содержатся в  . Записывают
. Записывают  .
.
Разность  , где
, где  – универсальное множество, называется дополнением множества
– универсальное множество, называется дополнением множества 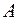 и обозначается символом
и обозначается символом  .
.
Типовой пример
Выполнить указанные операции  над множествами
над множествами  ,
,  ,
,  - подмножествами множества
- подмножествами множества  натуральных чисел.
натуральных чисел.
► Разность множеств  это множество, состоящее из элементов множества
это множество, состоящее из элементов множества  , не принадлежащих множеству
, не принадлежащих множеству  , то есть
, то есть  .
.
Множество  это множество, состоящее из элементов, принадлежащих хотя бы одному из множеств
это множество, состоящее из элементов, принадлежащих хотя бы одному из множеств  и
и  , то есть
, то есть  =
=  .
.
Множество  состоит из элементов множества
состоит из элементов множества  , не принадлежащих
, не принадлежащих  , то есть
, то есть  .
.
Множество  состоит из элементов, принадлежащих и множеству
состоит из элементов, принадлежащих и множеству  =
=  , и множеству
, и множеству  , то есть
, то есть  =
=  .◄
.◄
2. Декартово произведение. Соответствия
Пусть  и
и 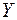 – произвольные множества. Пару
– произвольные множества. Пару  элементов
элементов 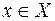 ,
,  , взятых в указанном порядке, будем называть упорядоченной парой, считая при этом, что
, взятых в указанном порядке, будем называть упорядоченной парой, считая при этом, что  тогда и только тогда, когда
тогда и только тогда, когда  . Декартовым произведением
. Декартовым произведением 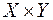 двух множеств
двух множеств  и
и 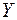 называется множество всех упорядоченных пар
называется множество всех упорядоченных пар  :
:
 .
.
Пусть, например,  – множество всех вещественных чисел. Тогда декартов квадрат
– множество всех вещественных чисел. Тогда декартов квадрат  есть просто множество всех декартовых координат точек плоскости относительно заданных координатных осей. Аналогичным образом можно было бы ввести декартово произведение
есть просто множество всех декартовых координат точек плоскости относительно заданных координатных осей. Аналогичным образом можно было бы ввести декартово произведение  трех множеств, четырех и т.д. При
трех множеств, четырех и т.д. При  пишут сокращенно
пишут сокращенно  вместо
вместо 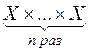 и говорят об
и говорят об  -й декартовой степени множества
-й декартовой степени множества  . Элементами
. Элементами  являются упорядоченные наборы
являются упорядоченные наборы  . Так, например, множество
. Так, например, множество  называется n - мерным арифметическим пространством; в частности, 1-мерное арифметическое пространство R называется числовой прямой, 2-мерное пространство R 2 — числовой плоскостью, 3-мерное пространство R 3 — числовым пространством.
называется n - мерным арифметическим пространством; в частности, 1-мерное арифметическое пространство R называется числовой прямой, 2-мерное пространство R 2 — числовой плоскостью, 3-мерное пространство R 3 — числовым пространством.
Пример
,,.
Если в декартовом произведении используются множества бесконечные, то  нельзя задать в виде конечного множества пар элементов, как в предыдущем примере. Тогда декартово произведение
нельзя задать в виде конечного множества пар элементов, как в предыдущем примере. Тогда декартово произведение  удобнее изобразить с помощью чертежа, где элементы
удобнее изобразить с помощью чертежа, где элементы  из множества
из множества  откладываются на горизонтальной прямой, а элементы
откладываются на горизонтальной прямой, а элементы  из множества
из множества  на вертикальной прямой, пересекающей первую под прямым углом в точке 0.
на вертикальной прямой, пересекающей первую под прямым углом в точке 0.
Пример

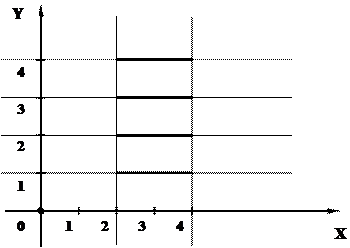 |
Если в декартовом произведении  множеств
множеств  и
и  выбрано некоторое подмножество упорядоченных пар
выбрано некоторое подмножество упорядоченных пар 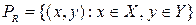 , то говорят, что задано соответствие
, то говорят, что задано соответствие  . Обозначается:
. Обозначается:  . Множество
. Множество  называется графиком соответствия
называется графиком соответствия  . Если множество
. Если множество  отложить на горизонтальной оси,
отложить на горизонтальной оси,  - на вертикальной, то множество пар
- на вертикальной, то множество пар 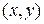 , удовлетворяющих соответствию
, удовлетворяющих соответствию  , является геометрической иллюстрацией графика соответствия.
, является геометрической иллюстрацией графика соответствия.
 Пример
Пример
Пусть  ,
,  :
:  , тогда
, тогда  =
= 

 | |||
 |
Если пары 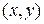 соответствия
соответствия  обозначить точками и стрелкой от элемента
обозначить точками и стрелкой от элемента  из множества
из множества  к элементы
к элементы  из множества
из множества  соединить те и только те пары, для которых выполняется
соединить те и только те пары, для которых выполняется  , то говорят, что построен граф соответствия
, то говорят, что построен граф соответствия  .
.
Областью отправления в соответствии  называется множество
называется множество  , множество
, множество  - это область прибытия соответствия.
- это область прибытия соответствия.
Соответствие 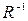 между множествами
между множествами  и
и  такое, что
такое, что  истинно тогда и только тогда, когда истинно
истинно тогда и только тогда, когда истинно  , называется обратным.
, называется обратным.
Соответствие  , график которого является дополнением к графику соответствия
, график которого является дополнением к графику соответствия  до декартова произведения
до декартова произведения  , называется соответствием, противоположным данному соответствию
, называется соответствием, противоположным данному соответствию  .
.
Пример
Для множеств  и
и  установлено соответствие
установлено соответствие  :
:  .
.
1) Графиком соответствия  является множество
является множество  .
.
 | |||||
 | |||||
3) Обратное соответствие 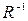 для
для  :
:  , если
, если  . Если
. Если  , то график обратного соответствия
, то график обратного соответствия  .
.
4) Если  - график данного соответствия
- график данного соответствия  ,
,  =
=
 то график соответствия
то график соответствия  , противоположного соответствию
, противоположного соответствию  :
:  =
=  .
.