Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Типовые примеры. Построить графики данных функций, исходя из основных элементарных функций
|
|
Построить графики данных функций, исходя из основных элементарных функций. Указать их области определения и области значений. Проверить, являются ли функции четными, нечетными или периодическими. В случае периодичности найти период:
► 1)  . Преобразуем данную функцию к виду
. Преобразуем данную функцию к виду  В качестве исходного возьмем график функции
В качестве исходного возьмем график функции  Имеем k =2 (сжатие в 2 раза вдоль оси Ox);
Имеем k =2 (сжатие в 2 раза вдоль оси Ox); 
 раза вдоль оси Oy c последующей симметрией относительно оси Ox).
раза вдоль оси Oy c последующей симметрией относительно оси Ox).
На рисунке изображены последовательные преобразования, приводящие к построению искомого графика.


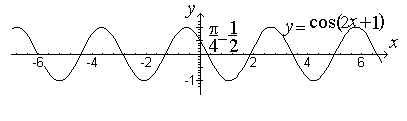


Очевидно, что данная функция определена на всей числовой прямой, т.е. 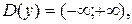 и
и  для всех x, т.е.
для всех x, т.е. 
Так как график не симметричен ни относительно оси Ox, ни относительно начала координат, функция не является ни четной, ни нечетной. Из периодичности функции  с периодом
с периодом  следует периодичность данной функции с периодом
следует периодичность данной функции с периодом 
2)  .
.
► Построим сначала график функции  . Так как |- x | = | x |, то эта функция четная, и ее график получается из графика функции
. Так как |- x | = | x |, то эта функция четная, и ее график получается из графика функции  симметрией относительно оси Oy и сжатием в 6 раз вдоль оси Oy, поскольку
симметрией относительно оси Oy и сжатием в 6 раз вдоль оси Oy, поскольку  .
.

| 
|

|
Искомый график образуется из полученного графика сдвигом на 2 единицы вправо, так как а =2.

Поскольку график функции  не симметричен ни относительно оси Oy, ни относительно начала координат, функция не является ни четной, ни нечетной. По графику видно, что функция непериодична,
не симметричен ни относительно оси Oy, ни относительно начала координат, функция не является ни четной, ни нечетной. По графику видно, что функция непериодична, 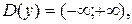
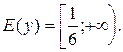
3) С помощью преобразования графика гиперболы 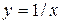 построить график функции
построить график функции  .
.
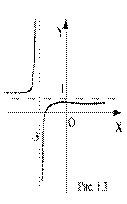
► Сначала необходимо выделить «целую часть» данной дробно-рациональной функции:  .
.
Далее последовательно выполняются следующие действия:
1) построить график функции  ;
;
2) сдвинуть его на 3 единицы влево по оси OX (получить график функции  );
);
3) полученный график симметрично отобразить относительно оси OX (график функции  );
);
5) сдвинуть его на единицу вверх вдоль оси OY (график заданной функции).
Результат построений можно видеть на рисунке 1.1.