Введение. Понятие о сезонных индексах.

Расчетно-графическое задание

Исследование корректности применения построенных разными методами доверительных интервалов для прогноза временного ряда при различных исходных распределениях значений временного ряда

Исходные данные и формализация задачи

Введение. Понятие о сезонных индексах.

Рассматриваются данные временных рядов, полученных в результате наблюдения за некоторыми реальными объектами (например, помесячный объем выручки пивоваренного завода, объем продаж киоска с мороженным). Предполагаем, что во временном ряде не наблюдается долгосрочной тенденции, но имеют место периодические изменения. В этом случае модель временного ряда должна содержать в себе функцию сезонности. Для построения функции сезонности существует множество подходов, но все они предполагают, что функция является периодической. Часто период сезонной функции можно определить из постановки задачи. Например, при рассмотрении ежеквартальных данных по потреблению тепловой энергии, очевидно, что период сезонных колебаний равен году, а количество сезонов 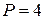. Если же данные по потреблению тепловой энергии представлены за каждый месяц, то период по-прежнему равен одному году, а количество сезонов . Предполагаем, что у нас в наличии имеются данные за пять периодов. Причем данные представлены не в исходном, а уже в некотором агрегированном виде.

В качестве примера на рис.1 показаны объемы потребления кефира в некотором супермаркете для каждого года и среднее значение за 5 лет. Год равен дробному количеству 52, 14 недель, но для упрощения расчетов он полагался равным целому числу 52 неделям, а неполная последняя неделя года переносилась на первую неделю следующего. То есть в данном случае .

Рисунок 1.

 

В задании на РГЗ будет дана информация именно об усредненных индексах (соответствует темной толстой линии на рисунке), и в данной работе мы рассматриваем самый простой способ задания функции сезонности – табличный.

 

Табличное представление сезонной функции

Номер сезона			…	Р
Сезонный индекс			…

 

Традиционно предполагают, что все сезонные воздействия за период взаимопогашаются:

 

.

Учитывая это условие и принимая во внимание тот факт, что реальные временные ряды, как правило, имеют ненулевые математические ожидания, целесообразно рассматривать модель вида

(другая общепринятая форма записи этой же модели - ).В этой модели 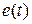- нерегулярная, случайная составляющая временного ряда. Обычно предполагают, что 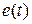это независимые(при различных значениях ) величины, подчиняющиеся нормальному закону распределения с нулевым математическим ожиданием и некоторой известной дисперсией.

Оценивание сезонных индексов 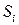как средних отклонений элементов временного ряда от оценки математического ожидания осуществляется согласно формуле:

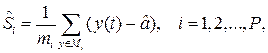
Где - множество моментов времени, соответствующих -му сезону, - количество элементов в множестве , - оценка математического ожидания временного ряда.