Бонусная часть РГЗ

Введение дополнительного метода построения доверительного интервала в случае распределения наблюдений по нормальному закону (1 бонусный балл).

По аналогии с тем, как это делалось в базовой части, только с использованием метода на основе МАРЕ.

Рассмотрение несимметричного закона, описанного в пункте b задания каждого варианта (1 бонусный балл)

Для распределения минимальных значений (при нулевом математическом ожидании)

,

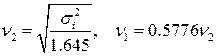Для распределения максимальных значений (при нулевом математическом ожидании)

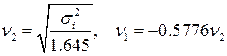, где 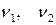- это первый и второй параметры распределения минимальных (и максимальных) значений.

1) вывод на экран параметров моделируемого распределения;

2) отображение графика функции плотности распределения при заданных параметрах распределения;

3) отображение графика функции распределения при заданных параметрах распределения;

Рассмотрение ситуации, описанной в пункте c задания каждого варианта (1 бонусный балл)

A. моделируем ошибки наблюдения в соответствии со смесью двух нормальных распределений, чтобы воспроизвести или двумодальный закон (тогда для первого закона в смеси берем математическое ожидание как 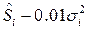, дисперсию как 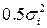, для второго закона в смеси берем математическое ожидание как 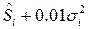, дисперсию как 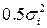, пропорции смеси 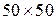), или ситуацию наличия выбросов (ситуация моделируется так же посредством смеси, но в качестве первого распределения берется исходный нормальный закон с математическим ожиданием, равным 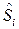, и дисперсией, равной , для второго закона в смеси берем математическое ожидание как 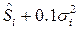(для правостороннего выброса) или 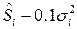(для левостороннего выброса), дисперсию как 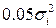, пропорции смеси 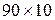). Что именно моделировать – двумодальность или выбросы, указывается в задании. Как моделировать смесь в соответствии с пропорцией смеси 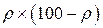: для этого нужно смоделировать две выборки – первую выборку объема 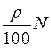( 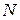– объем итоговой выборки, в случае выполняемого задания 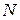=1000) в соответствии с первым законом распределения смеси, вторую выборку объема 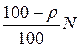– в соответствии со вторым законом распределения смеси, потом эти выборки объединяются в единую итоговую объема 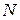. Надо понимать, что в жизни элементы этих двух выборок будут входить в итоговую выборку не последовательно, а, скорее всего, случайно, или в соответствии с некоторыми скрытыми закономерностями.

4) вывод на экран параметров моделируемого распределения;

5) отображение графика функции плотности распределения при заданных параметрах распределения;

6) отображение графика функции распределения при заданных параметрах распределения;