Аналитическая часть, выполняемая до проведения моделирования. На основании информации о математических ожиданиях , приведенных в задании, формируем вектор дисперсий

На основании информации о математических ожиданиях 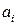, приведенных в задании, формируем вектор дисперсий 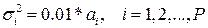. На основании этой информации строим, используя метод, опирающийся на правило двух сигм, доверительные интервалы для каждого сезона. При этом вначале мы используем максимальную информацию о данных (пункт Б), и полученные доверительные интервалы при моделировании будут использоваться для проверки корректности моделирования, а потом используем общий подход, предполагая, что распределение ошибок для всех наблюдений (то есть для всех точек во всех сезонах) одинаково (пункт В).

На едином графике отображаем

А) математические ожидания 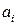, приведенные в задании, для всех сезонов ();

Б) доверительные интервалы, полученные по правилу двух сигм, но при использовании в качестве оценки дисперсии для каждого сезона с которой моделировались псевдо реальные значения показателей;

В) построение доверительных интервалов по классическому правилу двух сигм. Если бы мы вычисляли оценку дисперсии по исходным данным, то она бы совпала со средним арифметическим оценок дисперсий . И именно эта усредненная дисперсия используется, когда применяется правило «двух сигм» в данном, классическом, варианте.

Полученный график используется для визуализации доверительных интервалов, построенных разными методами.