Односторонние пределы

До сих пор мы рассматривали определение предела функции, когда x→ a произвольным образом, т.е. предел функции не зависел от того, как располагалось x по отношению к a, слева или справа от a. Однако, довольно часто можно встретить функции, которые не имеют предела при этом условии, но они имеют предел, если x→ a, оставаясь с одной стороны от а, слева или справа (см. рис.). Поэтому вводят понятия односторонних пределов.

Если f(x) стремится к пределу b при x стремящемся к некоторому числу a так, что x принимает только значения, меньшие a, то пишут и называют bпределом функции f(x) в точке a слева.

Таким образом, число b называется пределом функции y=f(x) при x→ a слева, если каково бы ни было положительное число ε, найдется такое число δ (меньшее a), что для всех выполняется неравенство .

Аналогично, если x→ a и принимает значения большие a, то пишут 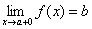и называют b пределом функции в точке а справа. Т.е. число b называется пределом функции y=f(x) при x→ a справа, если каково бы ни было положительное число ε, найдется такое число δ (большее а), что для всех 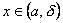выполняется неравенство .

Заметим, что если пределы слева и справа в точке a для функции f(x) не совпадают, то функция не имеет предела (двустороннего) в точке а.