
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функции. Их свойства
|
|
Определение 1. Функция 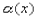 называется бесконечно малой (б.м.) функцией при
называется бесконечно малой (б.м.) функцией при 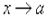 , если ее предел при
, если ее предел при  равен нулю.
равен нулю.
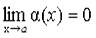 < => "
< => "  $
$  , для всех х, удовлетворяющих неравенству
, для всех х, удовлетворяющих неравенству  , будет выполняться неравенство
, будет выполняться неравенство  .
.
Определение 2. Функция  называется бесконечно большой (б.б.) функцией при
называется бесконечно большой (б.б.) функцией при 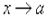 , если ее предел при
, если ее предел при  равен +¥ (-¥).
равен +¥ (-¥).
Пример. Функция  при
при  - б.м., при
- б.м., при  - б.б., при
- б.б., при  не является ни б.б. ни б.м.
не является ни б.б. ни б.м.
Теорема 1 (о связи предела и бесконечно малой функции). Если функция  имеет предел
имеет предел 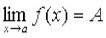 , то разность между функцией и значением предела есть функция, бесконечно малая при
, то разность между функцией и значением предела есть функция, бесконечно малая при  .
.
Доказательство. Необходимо показать, что
 < => f(x)-A б.м. функция при
< => f(x)-A б.м. функция при  .
.
Так как  , то
, то
" 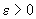 $
$ 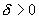 , для
, для  будет выполняться неравенство
будет выполняться неравенство  .
.
Сравним это с определением б. м. функции:
"  $
$ 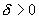 , для
, для  будет выполняться неравенство
будет выполняться неравенство  .
.
Сравнивая определения предела функции и б. м. функции, видим, что f(x)-A - б.м. при 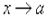 .
.
Теорема 2. Алгебраическая сумма конечного числа бесконечно малых при 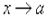 функций есть функция бесконечно малая при
функций есть функция бесконечно малая при  .
.
Доказательство. Пусть  - б.м. функции при
- б.м. функции при 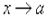 .
.
Надо доказать, что  есть б.м. функция при
есть б.м. функция при  .
.
Возьмем e> 0, тогда и  .
.
 Так как
Так как  - б.м. при
- б.м. при  , $
, $  ,
,  ,
,  ;
;
|
так как  - б.м. при
- б.м. при  , $
, $  ,
,  ,
, 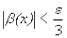 ;
;
так как  - б.м. при
- б.м. при  , $
, $  ,
,  ,
,  .
.
Возьмем  , тогда при
, тогда при 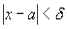 будут выполняться все три неравенства (2.1) одновременно.
будут выполняться все три неравенства (2.1) одновременно.
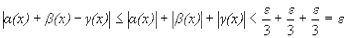 .
.
Итак, для " e> 0 мы нашли  такое, что при всех
такое, что при всех  выполняется неравенство
выполняется неравенство  , =>
, =>  есть б.м. функция при
есть б.м. функция при 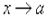 .
.
Теорема 3. Произведение бесконечно малой при  функции на ограниченную в некоторой окрестности точки а функцию есть бесконечно малая функция при
функции на ограниченную в некоторой окрестности точки а функцию есть бесконечно малая функция при 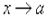 .
.
Доказательство. 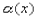 - б. м. при
- б. м. при  функция;
функция;
f(x) - ограниченная в некоторой окрестности точки а функция.
Докажем, что 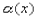 · f(x) – б. м. функция при
· f(x) – б. м. функция при  .
.
Поскольку f(x) - ограниченная в некоторой окрестности точки а функция, то $ 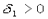 и $ К такие, что при " х
и $ К такие, что при " х
|
 Þ | f(x) | < К.
Þ | f(x) | < К.
Возьмем произвольное e> 0 и рассмотрим число  ,
,
так как 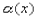 - б. м. при
- б. м. при  функция, $
функция, $  , что " х:
, что " х:
|
 Þ |
Þ | 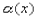 |<
|<  .
.
Возьмем  , тогда при
, тогда при  будут выполняться оба неравенства (2.2) и (2.3) одновременно.
будут выполняться оба неравенства (2.2) и (2.3) одновременно.
 <
< 
Итак, для " e> 0 мы нашли  такое, что при всех х, удовлетворяющих
такое, что при всех х, удовлетворяющих  , выполняется неравенство |
, выполняется неравенство |  · f(x) |< e, =>
· f(x) |< e, =>  · f(x) – б. м. функция при
· f(x) – б. м. функция при 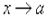 .
.
Теорема 4. Произведение конечного числа бесконечно малых при 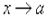 функций есть функция, бесконечно малая при
функций есть функция, бесконечно малая при  .
.
Теорема 5 (о связи бесконечно малой и бесконечно большой функций). Если  - б. м. при
- б. м. при  функция и
функция и  ¹ 0 в некоторой окрестности точки а, то функция
¹ 0 в некоторой окрестности точки а, то функция  есть б. б. функция при
есть б. б. функция при  .
.
Если  - при
- при  б. б. функция, то функция
б. б. функция, то функция  есть б. м. функция при
есть б. м. функция при 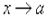 .
.