Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эквивалентные бесконечно малые
|
|
Функции 
и 
называют бесконечно малыми при 
, если 
и 
Функции и называют эквивалентными бесконечно малыми при , если 
Очень удобно пользоваться заменой эквивалентных бесконечно малых при нахождении пределов. Замена производится на основе таблицы.
Таблица эквивалентных бесконечно малых.
Пусть - бесконечно малая при .
Эквивалентность всех величин таблицы можно доказать, основываясь на равенстве .
Пример.
Доказать эквивалентность бесконечно малых величин 
и .
Решение.
Вычислим предел отношения этих величин 
Используя одно из свойств логарифма получим 
Поэтому предел примет вид:
Так как функция логарифма непрерывна на области определения, то можно воспользоваться свойством предела непрерывных функций и поменять местами знак предельного перехода и знак функции логарифма:
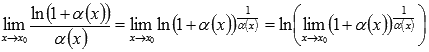
Проведем замену переменных 
. Так как - бесконечно малая функция при , то , следовательно, 
.
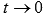Поэтому предел примет вид:
Полученная единица доказывает эквивалентность исходных бесконечно малых величин. В последнем переходе мы использовали второй замечательный предел.
Таблица эквивалентных бесконечно малых очень сильно ускоряет процесс решения, хотя без нее, конечно, можно обойтись. Вопрос – нужно ли только.
Пример.
Найти предел 
Решение.
Подставляем значение:
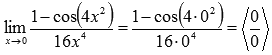
Пришли к неопределенности ноль делить на ноль. Эта неопределенность указывает на то, что и в числителе и в знаменателе находятся бесконечно малые функции. Обратимся к таблице эквивалентных бесконечно малых: функция 
эквивалентна 
, следовательно, 
эквивалентна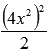 
.
Таким образом, после замены бесконечно малой функции ей эквивалентной, предел примет вид:
Без наличия таблицы эквивалентных бесконечно малых мы бы воспользовались, например, правилом Лопиталя:
Как вариант, можно было преобразовать функцию с использованием формул тригонометрии и применить первый замечательный предел:
№45
Пусть функция f (x) определена в некоторой окрестности O (x 0) точки x 0 (включая саму точку x 0).
Функция f (x) называется непрерывной в точке x 0, если существует lim x → x 0 f (x), равный значению функции f (x) в этой точке:
f (x) = f (x 0), | (1) |
т.е.
| " O (f (x 0)) $ O (x 0): x Î O (x 0) Þ f (x) Î O (f (x 0)). |
Замечание. Равенство (1) можно записать в виде:
f (x) = f (
x), |
т.е. под знаком непрерывной функции можно переходить к пределу.
Пусть Δ x = x − x 0 — приращение аргумента, Δ y = f (x) − f (x 0) — соответствующее приращение функции.