
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непрерывность функции на интервале и на отрезке
|
|
Определение 3.3 Пусть 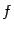 -- некоторая функция,
-- некоторая функция,  -- её область определения и
-- её область определения и  -- некоторый (открытый) интервал (может быть, с
-- некоторый (открытый) интервал (может быть, с 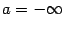 и/или
и/или  )7. Назовём функцию
)7. Назовём функцию 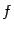 непрерывной на интервале
непрерывной на интервале  , если
, если 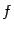 непрерывна в любой точке
непрерывна в любой точке  , то есть для любого
, то есть для любого  существует
существует  (в сокращённой записи:
(в сокращённой записи:

Пусть теперь  -- (замкнутый) отрезок в
-- (замкнутый) отрезок в  . Назовём функцию
. Назовём функцию  непрерывной на отрезке
непрерывной на отрезке  , если
, если 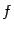 непрерывна на интервале
непрерывна на интервале  , непрерывна справа в точке
, непрерывна справа в точке  и непрерывна слева в точке
и непрерывна слева в точке 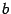 , то есть
, то есть



Пример 3.13 Рассмотрим функцию  (функция Хевисайда) на отрезке
(функция Хевисайда) на отрезке  ,
,  . Тогда
. Тогда  непрерывна на отрезке
непрерывна на отрезке  (несмотря на то, что в точке
(несмотря на то, что в точке  она имеет разрыв первого рода).
она имеет разрыв первого рода).

Рис.3.15.График функции Хевисайда
Аналогичное определение можно дать и для полуинтервалов вида  и
и  , включая случаи
, включая случаи 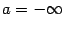 и
и  . Однако можно обобщить данное определение на случай произвольного подмножества
. Однако можно обобщить данное определение на случай произвольного подмножества 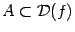 следующим образом. Введём сначала понятие индуцированной на
следующим образом. Введём сначала понятие индуцированной на  базы: пусть
базы: пусть 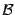 -- база, все окончания
-- база, все окончания  которой имеют непустые пересечения с
которой имеют непустые пересечения с  . Обозначим
. Обозначим  через
через  и рассмотрим множество всех
и рассмотрим множество всех  . Нетрудно тогда проверить, что множество
. Нетрудно тогда проверить, что множество  будет базой. Тем самым для
будет базой. Тем самым для 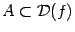 определены базы
определены базы  ,
,  и
и  , где
, где  ,
, 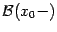 и
и  -- базы непроколотых двусторонних (соответственно левых, правых) окрестностей точки
-- базы непроколотых двусторонних (соответственно левых, правых) окрестностей точки  (их определение см. в начале текущей главы).
(их определение см. в начале текущей главы).
Определение 3.4 Назовём функцию  непрерывной на множестве
непрерывной на множестве 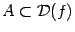 , если
, если

Нетрудно видеть, что тогда при  и при
и при  это определение совпадает с теми, что были выше даны специально для интервала и отрезка.
это определение совпадает с теми, что были выше даны специально для интервала и отрезка.
Напомним, что все элементарные функции непрерывны во всех точках своих областей определения и, следовательно, непрерывны на любых интервалах и отрезках, лежащих в их областях определения.
Поскольку непрерывность на интервале и отрезке определяется поточечно, имеет место теорема, которая является непосредственным следствием теоремы 3.1:
Теорема 3.5 Пусть  и
и 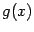 -- функции и
-- функции и  -- интервал или отрезок, лежащий в
-- интервал или отрезок, лежащий в  . Пусть
. Пусть 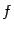 и
и 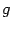 непрерывны на
непрерывны на  . Тогда функции
. Тогда функции  ,
,  ,
,  непpеpывны на
непpеpывны на  . Если вдобавок
. Если вдобавок  пpи всех
пpи всех 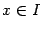 , то функция
, то функция  также непpеpывна на
также непpеpывна на  .
.
Из этой теоpемы вытекает следующее утвеpждение, точно так же, как из теоpемы 3.1 -- пpедложение 3.3:
Предложение 3.4 Множество  всех функций, непpеpывных на интеpвале или отpезке
всех функций, непpеpывных на интеpвале или отpезке  -- это линейное пpостpанство:
-- это линейное пpостpанство:

Более сложное свойство непрерывной функции выражает следующая теорема.
Теорема 3.6 (о корне непрерывной функции) Пусть функция 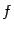 непрерывна на отрезке
непрерывна на отрезке  , причём
, причём  и
и  -- числа разных знаков. (Будем для определённости считать, что
-- числа разных знаков. (Будем для определённости считать, что  , а
, а  .) Тогда существует хотя бы одно такое значение
.) Тогда существует хотя бы одно такое значение  , что
, что  (то есть существует хотя бы один корень
(то есть существует хотя бы один корень  уравнения
уравнения 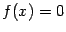 ).
).
Доказательство. Рассмотрим середину отрезка  . Тогда либо
. Тогда либо  , либо
, либо  , либо
, либо  . В первом случае корень найден: это
. В первом случае корень найден: это  . В остальных двух случаях рассмотрим ту часть отрезка, на концах которой функция
. В остальных двух случаях рассмотрим ту часть отрезка, на концах которой функция 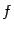 принимает значения разных знаков:
принимает значения разных знаков:  в случае
в случае  или
или  в случае
в случае  . Выбранную половину отрезка обозначим через
. Выбранную половину отрезка обозначим через 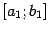 и применим к ней ту же процедуру: разделим на две половины
и применим к ней ту же процедуру: разделим на две половины  и
и  , где
, где  , и найдём
, и найдём  . В случае
. В случае  корень найден; в случае
корень найден; в случае  рассматриваем далее отрезок
рассматриваем далее отрезок  , в случае
, в случае  -- отрезок
-- отрезок  и т. д.
и т. д.
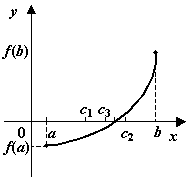
Рис.3.16.Последовательные деления отрезка пополам
Получаем, что либо на некотором шаге будет найден корень  , либо будет построена система вложенных отрезков
, либо будет построена система вложенных отрезков

в которой каждый следующий отрезок вдвое короче предыдущего. Последовательность  -- неубывающая и ограниченная сверху (например, числом
-- неубывающая и ограниченная сверху (например, числом 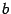 ); следовательно (по теореме 2.13), она имеет предел
); следовательно (по теореме 2.13), она имеет предел  . Последовательность
. Последовательность  -- невозрастающая и ограниченная снизу (например, числом
-- невозрастающая и ограниченная снизу (например, числом  ); значит, существует предел
); значит, существует предел  . Поскольку длины отрезков
. Поскольку длины отрезков  образуют убывающую геометрическую прогрессию (со знаменателем
образуют убывающую геометрическую прогрессию (со знаменателем  ), то они стремятся к 0, и
), то они стремятся к 0, и  , то есть
, то есть  . Положим теперь
. Положим теперь  . Тогда
. Тогда
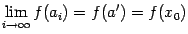 и
и 
поскольку функция 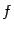 непрерывна. Однако, по построению последовательностей
непрерывна. Однако, по построению последовательностей  и
и  ,
,  и
и  , так что, по теореме о переходе к пределу в неравенстве (теорема 2.7),
, так что, по теореме о переходе к пределу в неравенстве (теорема 2.7),  и
и 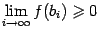 , то есть
, то есть  и
и  . Значит,
. Значит,  , и
, и  -- корень уравнения
-- корень уравнения 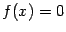 .
.
Пример 3.14 Рассмотрим функцию  на отрезке
на отрезке  . Поскольку
. Поскольку  и
и  -- числа разных знаков, то функция
-- числа разных знаков, то функция  обращается в 0 в некоторой точке
обращается в 0 в некоторой точке  интервала
интервала  . Это означает, что уравнение
. Это означает, что уравнение  имеет корень
имеет корень  .
.

Рис.3.17.Графическое представление корня уравнения 
Доказанная теорема фактически даёт нам способ нахождения корня  , хотя бы приближённого, с любой заданной наперёд степенью точности. Это -- метод деления отрезка пополам, описанный при доказательстве теоремы. Более подробно с этим и другими, более эффективными, способами приближённого нахождения корня мы познакомимся ниже, после того, как изучим понятие и свойства производной.
, хотя бы приближённого, с любой заданной наперёд степенью точности. Это -- метод деления отрезка пополам, описанный при доказательстве теоремы. Более подробно с этим и другими, более эффективными, способами приближённого нахождения корня мы познакомимся ниже, после того, как изучим понятие и свойства производной.
Заметим, что теорема не утверждает, что если её условия выполнены, то корень  -- единственный. Как показывает следующий рисунок, корней может быть и больше одного (на рисунке их 3).
-- единственный. Как показывает следующий рисунок, корней может быть и больше одного (на рисунке их 3).

Рис.3.18.Несколько корней функции, принимающей значения разных знаков в концах отрезка
Однако, если функция монотонно возрастает или монотонно убывает на отрезке, в концах которого принимает значения разных знаков, то корень -- единственный, так как строго монотонная функция каждое своё значение принимает ровно в одной точке, в том числе и значение 0.

Рис.3.19.Монотонная функция не может иметь более одного корня
Непосредственным следствием теоремы о корне непрерывной функции является следующая теорема, которая и сама по себе имеет очень важное значение в математическом анализе.
Теорема 3.7 (о промежуточном значении непрерывной функции) Пусть функция  непрерывна на отрезке
непрерывна на отрезке  и
и  (будем для определённости считать, что
(будем для определённости считать, что  ). Пусть
). Пусть  -- некоторое число, лежащее между
-- некоторое число, лежащее между  и
и  . Тогда существует такая точка
. Тогда существует такая точка  , что
, что  .
.

Рис.3.20.Непрерывная функция принимает любое промежуточное значение
Доказательство. Рассмотрим вспомогательную функцию 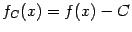 , где
, где  . Тогда
. Тогда  и
и 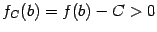 . Функция
. Функция  , очевидно, непрерывна, и по предыдущей теореме существует такая точка
, очевидно, непрерывна, и по предыдущей теореме существует такая точка  , что
, что 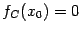 . Но это равенство означает, что
. Но это равенство означает, что  .
.
Заметим, что если функция не является непрерывной, то она может принимать не все промежуточные значения. Например, функция Хевисайда  (см. пример 3.13) принимает значения
(см. пример 3.13) принимает значения  ,
,  , но нигде, в том числе и на интервале
, но нигде, в том числе и на интервале  , не принимает, скажем, промежуточного значения
, не принимает, скажем, промежуточного значения  . Дело в том, что функция Хевисайда имеет разрыв в точке
. Дело в том, что функция Хевисайда имеет разрыв в точке  , лежащей как раз в интервале
, лежащей как раз в интервале  .
.
Для дальнейшего изучения свойств функций, непрерывных на отрезке, нам понадобится следующее тонкое свойство системы вещественных чисел (мы уже упоминали его в главе 2 в связи с теоремой о пределе монотонно возрастающей ограниченной функции): для любого ограниченного снизу множества  (то есть такого, что
(то есть такого, что  при всех
при всех  и некотором
и некотором  ; число
; число  называется нижней гранью множества
называется нижней гранью множества  ) имеется точная нижняя грань
) имеется точная нижняя грань  , то есть наибольшее из чисел
, то есть наибольшее из чисел  , таких что
, таких что  при всех
при всех  . Аналогично, если множество
. Аналогично, если множество  ограничено сверху, то оно имеет точную верхнюю грань
ограничено сверху, то оно имеет точную верхнюю грань  : это наименьшая из верхних граней
: это наименьшая из верхних граней  (для которых
(для которых  при всех
при всех  ).
).

Рис.3.21.Нижняя и верхняя грани ограниченного множества
Если  , то существует невозрастающая последовательность точек
, то существует невозрастающая последовательность точек  , которая стремится к
, которая стремится к  . Точно так же если
. Точно так же если 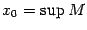 , то существует неубывающая последовательность точек
, то существует неубывающая последовательность точек  , которая стремится к
, которая стремится к  .
.
Если точка  принадлежит множеству
принадлежит множеству  , то
, то  является наименьшим элементом этого множества:
является наименьшим элементом этого множества:  ; аналогично, если
; аналогично, если  , то
, то  .
.
Кроме того, для дальнейшего нам понадобится следующая
Лемма 3.1 Пусть  -- непрерывная функция на отрезке
-- непрерывная функция на отрезке  , и множество
, и множество  тех точек
тех точек 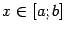 , в которых
, в которых  (или
(или  , или
, или 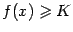 ) не пусто. Тогда в множестве
) не пусто. Тогда в множестве  имеется наименьшее значение
имеется наименьшее значение  , такое что
, такое что  при всех
при всех  .
.
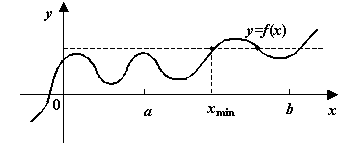
Рис.3.22.Наименьший аргумент, при котором функция принимает заданное значение
Доказательство. Поскольку  -- ограниченное множество (это часть отрезка
-- ограниченное множество (это часть отрезка  ), то оно имеет точную нижнюю грань
), то оно имеет точную нижнюю грань  . Тогда существует невозрастающая последовательность
. Тогда существует невозрастающая последовательность 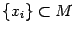 ,
,  , такая что
, такая что  при
при  . При этом
. При этом  , по определению множества
, по определению множества  . Поэтому, переходя к пределу, получаем, с одной стороны,
. Поэтому, переходя к пределу, получаем, с одной стороны,

а с другой стороны, вследствие непрерывности функции  ,
,

Значит,  , так что точка
, так что точка  принадлежит множеству
принадлежит множеству  и
и  .
.
В случае, когда множество  задано неравенством
задано неравенством  , мы имеем
, мы имеем  при всех
при всех  и по теореме о переходе к пределу в неравенстве получаем
и по теореме о переходе к пределу в неравенстве получаем

откуда  , что означает, что
, что означает, что  и
и  . Точно так же в случае неравенства
. Точно так же в случае неравенства 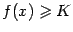 переход к пределу в неравенстве даёт
переход к пределу в неравенстве даёт

откуда 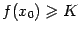 ,
,  и
и  .
.
Теорема 3.8 (об ограниченности непрерывной функции) Пусть функция  непрерывна на отрезке
непрерывна на отрезке  . Тогда
. Тогда 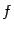 ограничена на
ограничена на  , то есть существует такая постоянная
, то есть существует такая постоянная  , что
, что  при всех
при всех 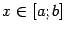 .
.
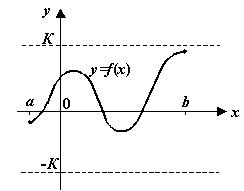
Рис.3.23.Непрерывная на отрезке функция ограничена
Доказательство. Предположим обратное: пусть  не ограничена, например, сверху. Тогда все множества
не ограничена, например, сверху. Тогда все множества  ,
,  ,
,  , не пусты. По предыдущей лемме в каждом из этих множеств
, не пусты. По предыдущей лемме в каждом из этих множеств  имеется наименьшее значение
имеется наименьшее значение  ,
,  . Покажем, что
. Покажем, что

Действительно,  . Если какая-либо точка из
. Если какая-либо точка из 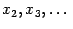 , например
, например  , лежит между
, лежит между  и
и  , то
, то

то есть 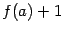 -- промежуточное значение между
-- промежуточное значение между  и
и  . Значит, по теореме о промежуточном значении непрерывной функции, существует точка
. Значит, по теореме о промежуточном значении непрерывной функции, существует точка  , такая что
, такая что  , и
, и  . Но
. Но  , вопреки предположению о том, что
, вопреки предположению о том, что  -- наименьшее значение из множества
-- наименьшее значение из множества  . Отсюда следует, что
. Отсюда следует, что  при всех
при всех  .
.
Точно так же далее доказывается, что  при всех
при всех  ,
,  при всех
при всех  , и т. д. Итак,
, и т. д. Итак,  -- возрастающая последовательность, ограниченная сверху числом
-- возрастающая последовательность, ограниченная сверху числом 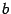 . Поэтому существует
. Поэтому существует  . Из непрерывности функции
. Из непрерывности функции  следует, что существует
следует, что существует 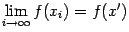 , но
, но  при
при  , так что предела не существует. Полученное противоречие доказывает, что функция
, так что предела не существует. Полученное противоречие доказывает, что функция  ограничена сверху.
ограничена сверху.
Аналогично доказывается, что  ограничена снизу, откуда следует утверждение теоремы.
ограничена снизу, откуда следует утверждение теоремы.
Очевидно, что ослабить условия теоремы нельзя: если функция не является непрерывной, то она не обязана быть ограниченной на отрезке (приведём в качестве примера функцию

на отрезке 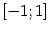 . Эта функция не ограничена на отрезке, так как при
. Эта функция не ограничена на отрезке, так как при  имеет точку разрыва второго рода, такую что
имеет точку разрыва второго рода, такую что  при
при  . Также нельзя заменить в условии теоремы отрезок интервалом или полуинтервалом: в качестве примера рассмотрим ту же функцию
. Также нельзя заменить в условии теоремы отрезок интервалом или полуинтервалом: в качестве примера рассмотрим ту же функцию  на полуинтервале
на полуинтервале  . Функция непрерывна на этом полуинтервале, но неограничена, вследствие того что
. Функция непрерывна на этом полуинтервале, но неограничена, вследствие того что 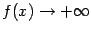 при
при  .
.
Поиск наилучших постоянных, которыми можно ограничить функцию сверху и снизу на заданном отрезке, естественным образом приводит нас к задаче об отыскании минимума и максимума непрерывной функции на этом отрезке. Возможность решения этой задачи описывается следующей теоремой.
Теорема 3.9 (о достижении экстремума непрерывной функцией) Пусть функция  непрерывна на отрезке
непрерывна на отрезке  . Тогда существует точка
. Тогда существует точка  , такая что
, такая что  при всех
при всех 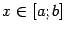 (то есть
(то есть  -- точка минимума:
-- точка минимума:  ), и существует точка
), и существует точка  , такая что
, такая что  при всех
при всех 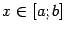 (то есть
(то есть  -- точка максимума:
-- точка максимума:  ). Иными словами, минимальное и максимальное8 значения непрерывной функции на отрезке существуют и достигаются в некоторых точках
). Иными словами, минимальное и максимальное8 значения непрерывной функции на отрезке существуют и достигаются в некоторых точках  и
и  этого отрезка.
этого отрезка.

Рис.3.24.Непрерывная на отрезке функция достигает максимума и минимума
Доказательство. Так как по предыдущей теореме функция  ограничена на
ограничена на  сверху, то существует точная верхняя грань значений функции на
сверху, то существует точная верхняя грань значений функции на  -- число
-- число 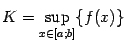 . Тем самым, множества
. Тем самым, множества  ,
,  ,...,
,...,  ,..., не пусты, и по предыдущей лемме в них есть наименьшие значения
,..., не пусты, и по предыдущей лемме в них есть наименьшие значения  :
:  ,
,  . Эти
. Эти  не убывают (доказывается это утверждение точно так же, как в предыдущей теореме):
не убывают (доказывается это утверждение точно так же, как в предыдущей теореме):

и ограничены сверху числом 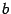 . Поэтому, по теореме о пределе монотонной ограниченной последовательности, существует предел
. Поэтому, по теореме о пределе монотонной ограниченной последовательности, существует предел  Так как
Так как  , то и
, то и
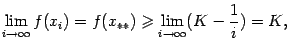
по теореме о переходе к пределу в неравенстве, то есть  . Но при всех
. Но при всех 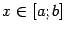
 , и в том числе
, и в том числе  . Отсюда получается, что
. Отсюда получается, что  , то есть максимум функции достигается в точке
, то есть максимум функции достигается в точке  .
.
Аналогично доказывается существование точки минимума.
В этой теореме, как и в предыдущей, нельзя ослабить условия: если функция не является непрерывной, то она может не достигать своего максимального или минимального значения на отрезке, даже будучи ограниченной. Для примера возьмём функцию

на отрезке 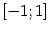 . Эта функция ограничена на отрезке (очевидно, что
. Эта функция ограничена на отрезке (очевидно, что  ) и
) и  , однако значение 1 она не принимает ни в одной точке отрезка (заметим, что
, однако значение 1 она не принимает ни в одной точке отрезка (заметим, что  , а не 1). Дело в том, что эта функция имеет разрыв первого рода в точке
, а не 1). Дело в том, что эта функция имеет разрыв первого рода в точке  , так что при
, так что при  предел
предел  не равен значению функции в точке 0. Далее, непрерывная функция, заданная на интервале или другом множестве, не являющемся замкнутым отрезком (на полуинтервале, полуоси) также может не принимать экстремального значения. В качестве примера рассмотрим функцию
не равен значению функции в точке 0. Далее, непрерывная функция, заданная на интервале или другом множестве, не являющемся замкнутым отрезком (на полуинтервале, полуоси) также может не принимать экстремального значения. В качестве примера рассмотрим функцию  на интервале
на интервале  . Очевидно, что функция непрерывна и что
. Очевидно, что функция непрерывна и что  и
и  , однако ни значения 0, ни значения 1 функция не принимает ни в какой точке интервала
, однако ни значения 0, ни значения 1 функция не принимает ни в какой точке интервала  . Рассмотрим также функцию
. Рассмотрим также функцию 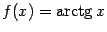 на полуоси
на полуоси  . Эта функция непрерывна на
. Эта функция непрерывна на  , возрастает, принимает своё минимальное значение 0 в точке
, возрастает, принимает своё минимальное значение 0 в точке  , но не принимает ни в какой точке максимального значения (хотя ограничена сверху числом
, но не принимает ни в какой точке максимального значения (хотя ограничена сверху числом  и
и 