Обратная матрица. 1. Матрица А называется невырожденной или неособенной, если

1. Матрица А называется невырожденной или неособенной, если

2. Матрица B называется обратной к матрице А, если

Обозначается,

3. Теорема (критерий существования обратной матрицы). Приведите формулировку теоремы.

4. Напишите обратные матрицы для следующих матриц.

5. Найдите матрицы, обратные к данным.

Решение.

Вычислим определитель матрицы А и, если он отличен от нуля, то обратная матрица существует.

обратная матрица существует.

Найдём алгебраические дополнения элементов матрицы

Тогда обратимая матрица имеет вид

6. Найдите обратные матрицы для следующих диагональных матриц.

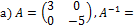
7. Транспонируйте матрицы и найдите обратные матрицы к транспонированным.

8. Найдите:

а) элементы матрицы если

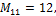
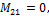
б) элементы матрицы 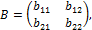если

c) элементы матрицы если

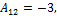
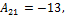
г) элементы матрицы 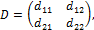если

9. Найдите:

а) элементы матрицы если и

б) элементы матрицы 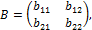если и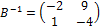

10. Найдите:

если ;

если ;

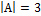если ,

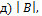если ,

если ,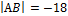

11. Решите матричные уравнения.

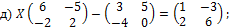
13. В трёх торговых точках проведена ревизия и получены следующие данные о количестве проданных товаров трёх видов (в условных единицах):

В кассе 1-го магазина обнаружено 31, 8 условной денежной единицы, 2-го – 154, 6; 3-го – 141, 1. Необходимо определить, по какой цене продавался каждый вид товара, чтобы сравнить эти цены, с имеющимися в накладных.

Решение.

Обозначим: – матрица-столбец стоимостей товаров;

– матрица продажи; – матрица-столбец

выручки по магазинам.

Тогда математическая модель задачи имеет вид: 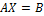. Решение задачи найдём, решив матричное уравнение, т.е. 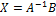. Продолжите решение задачи.