Ранг матрицы.

1. Пусть ненулевая матрица A имеет размерность 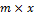и число k удовлетворяет условию 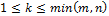. Выделим в матрице A k различных строк и k различных столбцов.

Минором k- того порядка матрицы A называется

2. Для матрицы 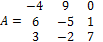вычислить миноры:

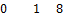
а) первого порядка:

б) второго порядка:

в) третьего порядка:

3. Рангом матрицы называется

Ранг нулевой матрицы равен

Ранг матрицы равен r, если

5. Найдите ранг матрицы A, если:

а) А- невырожденная квадратная матрица четвертого порядка;

б) А- ненулевая квадратная матрица второго порядка, определитель которого равен нулю;

в) А- квадратная матрица третьего порядка, определитель которой отличен от нуля.

6. Матрицы А и В называют эквивалентными, если

7. Укажите эквивалентные матрицы:

а) А матрица размерности и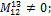

б) B – невырожденная квадратная матрица второго порядка;

в) С – вырожденная квадратная матрица второго порядка;

г) D – квадратная матрица четвертого порядка и все миноры третьего порядка этой матрицы равны нулю.

8. Элементарными преобразованиям матрицы называются

9. Элементарные преобразования: ранг матрицы.

Сделайте правильный выбор

10. Укажите эквивалентные матрицы:

а) .

11. Укажите способы нахождения ранга матрицы.

a)

б)

12. Найдите ранги матриц методом элементарных преобразований.

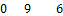
13. При каком значении параметра α ранг матрицы:

равен двум?

равен трём?

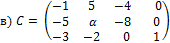равен двум?

14. Объясните в чём состоит суть метода окаймления миноров.

15. Найдите ранги матриц методом окаймления миноров.

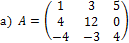
1

16. Матрица A имеет размерность и ранг матрицы равен трём. Укажите порядки её миноров от нуля.

17. Матрица B имеет размерность 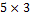и ранг матрицы равен двум.

Вычислите минор третьего порядка .

18. Матрица C имеет размерность и ранг матрицы равен трём.

Верно ли утверждение, что все миноры четвёртого порядка равны нулю?

19. Матрица D является квадратной матрицей четвёртого порядка и ранг матрицы равен трём. Вычислите определитель матрицы D.

20. Матрица F невырожденная квадратная матрица n- порядка и rang(A)=4. Определите размерность матрицы.

21. Теорема (основное свойство ранга матрицы). Приведите формулировку теоремы.

22. Матрица A имеет размерность и . Найдите ранг матрицы и укажите линейно независимые строки и столбцы матрицы.

23. Матрица A имеет размерность 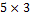. Найдите ранг и укажите линейно независимые строки и столбцы матрицы.

24. Матрица A имеет размерность . Найдите ранг и укажите линейно независимые столбцы матрицы.

25. Матрица A имеет размерность , rang(A)=2 и 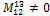. Укажите линейно независимые строки и столбцы.

26. Матрица A имеет размерность и ранг матрицы равен двум.

Вычислите миноры третьего порядка матрицы A.

27. Матрица A имеет размерность 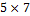и ранг матрицы равен трём. Укажите порядки её миноров: а) отличных от нуля; б) равных нулю.

а)

б)

28. Матрица A имеет размерность 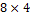и ранг матрицы равен двум. Укажите порядки её миноров: а) отличных от нуля; б) равных нулю.

а)

б)

29. Матрица A имеет размерность 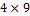и ранг матрицы равен трём. Укажите верные утверждения:

а) все миноры третьего порядка этой матрицы отличны от нуля;

б) все миноры четвёртого порядка этой матрицы равны нулю;

в) минор четвёртого порядка ;

г) существует минор третьего порядка, отличный от нуля;