
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные задачи.
|
|
1. Числовой прямой или числовой осью называется
2. Декартовой системой координат называются
Горизонтальная ось называется
Вертикальная ось называется
3. Координатами точки M на плоскости называется
4. Расстояние между двумя точками плоскости A(x1; y1), B(x2; y2) находится по формуле
5. Найдите расстояние между точками:
а) A(3; 5), B(7; 5);
б) A(-4; 1), B(0; 2);
в) A(6; -2), B(-6; 8);
6. Теорема (деление отрезка в данном отношении). Приведите формулировку теоремы.
7. Если точка С (x0; y0) делит отрезок AB, A(x1; y1), B(x2; y2) пополам, то координаты точки С находятся по формуле
8. Точка С (x0; y0) делит отрезок AB пополам, то координаты точки С, если:
а) A(-5; 2), B(3; 4);
б) A(8; -1), B(3; 6);
в) A(0; 4), B(-2; 7);
9. Отрезок AB, A(-4; 5), B(0; 3) разделён на три равные части точками
C и D. Найдите координаты: а) точки C; б) точки D.
а)
б)
10. Отрезок AB, A(2; 7), B(-3; 6) разделён на четыре равные части точками
C, D, F. Найдите координаты:
а) точки C;
б) точки D;
в) точки F;
11. Углом наклона прямой l к оси ox называется
Обозначается
12. Угловым коэффициентом называется
Обозначается
13. Определите углы наклона следующих прямых:
а) 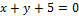 ;
;
б)  ;
;
в)  ;
;
г)  .
.
14. Теорема. Если прямая l не параллельна оси oy и на этой прямой заданы
две точки A(x1; y1), B(x2; y2), то угловой коэффициентов прямой находится
по формуле
15. Найдите угловые коэффициенты прямых, если известно, что прямые
проходят через точки.
а) A(-5; 3), B(-1; 7);
б) A(8; 0), B(-4; 5);
в) A(0; 6), B(3; 4);
г) A(-2; 7), B(0; -3);
16. Напишите:
а) уравнение прямой с угловым коэффициентом
б) общее уравнение прямой
в) уравнение прямой, проходящей через точку в данном направлении
г) уравнение прямой, проходящей через две данные точки
д) уравнение прямой «в отрезках на осях»
е) нормальное уравнение прямой
17. Углом между двумя прямыми l1 и l2 называется
18. Найдите угол между прямыми  ,
, 
19. Теорема (условие параллельности двух прямых). Приведите формулировку теоремы.
20. Теорема (условие перпендикулярности двух прямых). Приведите формулировку теоремы.
21. Напишите  прямых l1 и l2, заданных своими общими уравнениями.
прямых l1 и l2, заданных своими общими уравнениями.
а)
б)
22. Укажите параллельные прямые:
а)  ,
,  ;
;
б)  ,
,  ;
;
в) 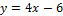 ,
,  ;
;
г)  ,
,  .
.
23. Укажите перпендикулярные прямые:
а)  ,
,  ;
;
б)  ,
,  .
.
в)  ,
,  ;
;
г)  ,
,  .
.
24. Составление уравнения прямой, если известно, что:
а) прямая проходит через точку A(0; 3) параллельно оси ox;
б) прямая проходит через точку A(-4; 0) перпендикулярно оси ox;
в) прямая проходит через точку A(-3; 5) параллельно биссектрисе первого и третьего координатных углов;
г) прямая проходит через точку A(2; -1) перпендикулярно биссектрисе второго и четвёртого координатных углов;
д) прямая проходит через точку A(-4; 0) параллельно  ;
;
е) прямая проходит через точку A(2; -5) перпендикулярно 
25. Отрезок AB, A(-2; 3), B(1; -5) разделён на четыре равные части точками
C, D, E. Найдите уравнение прямых, проходящих через точки деления, перпендикулярно AB.
26. Отрезок AB, A(4; -3), B(0; 1) разделён на три равные части точками
C, D. Найдите уравнение прямых, проходящих через точки деления, перпендикулярно AB.
27. При каком значении параметра a прямые 
и  перпендикулярны?
перпендикулярны?
28. При каком значении параметра a прямые  и
и  параллельны?
параллельны?
29. Расстояние от точки C (x0; y0) до прямой l∶ Ax+By+C=0 находится по формуле
30. Найдите расстояние от точки C до прямой Ax+By+C=0, если:
а) C(-4; 5), 

б) C(0; 7), 
в) C(-2; 6), 
31. Треугольник задан вершинами:
а) A(-1; 1), B(6; 4), C(3; -2); б) A(-1; 1), B(6; 4), C(3; -2);
в) A(-2; 1), B(7; 4), C(-6; 2);
Постройте треугольник.
Найдите:
а) длины сторон; б) уравнение сторон;
в) уравнение медиан; г) внутренние углы треугольника
д) длины медиан; е) длины высот;
ж) точку пересечения высот треугольника;
з) точку пересечения медиан треугольника;
и) площадь треугольника.
32. Проверьте, что точки A(-2; -2), B(3; -1), C(7; 7), D(3; 1); являются вершинами трапеции, и составьте уравнения средней линии и диагоналей трапеции.
33. Найдите ординату точки C(5; y), если известно, что прямая AB,
A(-2; -2), B(3; -1) проходит через эту точку.
34. Даны две точки A(-3; 1), B(3; -7). На оси ординат найдите такую точку M, что бы прямые AM и MB были перпендикулярны.
35. Диагонали ромба, равны 10 и 4 единицам длины, приняты за оси координат. Напишите уравнения сторон ромба.
36. Найдите величины отрезков, отсекаемых на осях координат прямыми:
а) 
б) 
в) 
г) 
37. Даны уравнения сторон треугольника:  ,
,
 ,
, 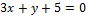 . Найдите координаты его вершин.
. Найдите координаты его вершин.
38. Даны вершины четырёхугольника: A(-9; 0), B(-3; 6), C(3; 4), D(6; -3).
Найдите точку пресечения его диагоналей AC и BD и найдите угол между ними.
39. Найдите координаты вершин ромба, если известны уравнения двух его сторон: 2  ,
,  , и уравнение одной из его диагоналей
, и уравнение одной из его диагоналей  .
.
40. Даны уравнение двух смежных сторон параллелограмма:
 ,
, 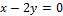 и точка пересечения его диагоналей M(3; -1).
и точка пересечения его диагоналей M(3; -1).
Напишите уравнения двух других сторон параллелограмма.
Кривые второго порядка.
Окружность, эллипс, гипербола и парабола.
1. Общим уравнением второго порядка называется уравнение вида
2. Укажите условия, при которых уравнение
 ,
, 
является уравнением:
а) эллиптического типа;
б) гиперболического типа;
в) параболического типа.
3. Напишите:
а)каноническое уравнение окружности; б)нормальное уравнение окружности. Объясните смысл обозначений.
а)
б)
4. Напишите уравнение окружности, центр которой находится в точке
C(a; b) и радиус равен R:
а) 


б) 


в) 


в) 


5. Окружность задана уравнением. Определите координаты центра и радиус окружности:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  .
.
6. Напишите уравнение окружности, диаметр которой:
а)  , A(0; -2), B(0; 2);
, A(0; -2), B(0; 2);
б)  , A(1; -4), B(3; 6);
, A(1; -4), B(3; 6);
7. Эллипсом называется
8. Напишите каноническое уравнение эллипса. Объясните смысл букв.
9. Определите длины полуосей эллипса, заданного своим каноническим уравнением:
а)  ;
;
б)  .
.
10. Вершина эллипса называются
11. Дано уравнение эллипса. Определите координаты его вершин:
а)  ;
;
б)  ;
;
в)  .
.
12. Напишите каноническое уравнение эллипса, если известны координаты двух его вершин:
а) A2(9; 0), B2(0; 4);
б) A1(-7; 0), B1(0; -5).
13. Напишите каноническое уравнение эллипса, если известны:
а) длины его большой и малой полуосей 6, 2;
б) длины его большой и малой осей 18, 10.
14. Гиперболой называется
15. Напишите каноническое уравнение гиперболы. Объясните смысл обозначений.
16. Найдите координаты вершин гиперболы, заданной своими каноническим уравнением:
а)  ;
;
б)  ;
;
17. Напишите уравнение осей симметрии гиперболы, заданной уравнением  .
.
18. Напишите каноническое уравнение гиперболы, если известны:
а) длины его действительной и мнимой полуосей 5, 2;
б) длины его действительной и мнимой осей 12, 8.
19. Напишите каноническое уравнение гиперболы, если известны координаты её вершины A(12; 0) и расстояние между фокусами 26.
20. Дано уравнение гиперболы  . Определите координаты фокусов гиперболы.
. Определите координаты фокусов гиперболы.
21. Дано уравнение гиперболы  . Напишите уравнения её асимптот.
. Напишите уравнения её асимптот.
22. Известны координаты вершины и фокуса гиперболы A1(12; 0), F1(13; 0).
Напишите каноническое уравнение гиперболы.
23. Параболой называется
24. Напишите каноническое уравнение параболы, осью симметрии которой является:
а) ось ox;
б) ось oy;
25. Напишите уравнение директрисы и оси симметрии параболы, определите координаты фокуса, если:
а) 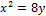 ;
;
б))  ;
;
в)  ;
;
г)  ;
;
26. Найдите точки пересечения параболы  с прямой
с прямой  .
.
27. Дано уравнение параболы. Определите координаты вершины и фокуса параболы.
а) 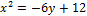 ;
;
б)  .
.