Билет 3. Методы вычисления неопределенного интеграла: замена переменных, интегрирование по частям.

Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов: а), где – монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае:; б), где U – новая переменная. Формула замены переменной при такой подстановке:. Интегрирование по частям

Нахождение интеграла по формуле 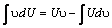называется интегрированием по частям. Здесь U = U (х), υ =υ (x) непрерывно дифференцируемые функции от х. С помощью этой формулы нахождение интеграла сводится к отысканию другого интеграла 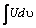, ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
При этом за υ берется такая функция, которая при дифференцировании упрощается, а за dU – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
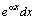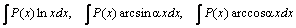Так например, для интегралов вида , , , где P (x) – многочлен, за υ следует принять P (x), а за dU соответствует выражение , . Для интегралов вида за υ принимаются соответственно функции , а за 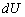– выражение P (x) dx.