Билет 13с. Линейные неоднородные дифференциальные уравнения второго порядка.

Общее решение y линейного неоднородного дифференциального уравнения

уравнения на интервале X с непрерывными на том же промежутке X коэффициентами и функцией f(x)представляет собой сумму 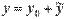, где y0 - общее решение соответствующего ЛОДУ 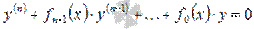, а - какое-нибудь частное решение исходного ЛНДУ.

Таким образом,

y0=C1⋅ y1+C2⋅ y2 - общее решение дифференциального уравнения , где y1 и y2 – его линейно независимые частные решения,

а 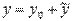- общее решение уравнения , где - любое из его частных решений, а y0 - общее решение соответствующего ЛОДУ.

При решении линейного неоднородного дифференциального уравнения второго порядка , если удалось найти y1 и y2, то можно не заниматься подбором . Общее решение ЛНДУ может быть найдено методом вариации произвольных постоянных.

В этом случае общее решение ЛОДУ имеет вид y0 = C1 ⋅ y1 + C2 ⋅ y2. Варьируя произвольные постоянные, в качестве общего решения ЛНДУ принимаемy0 = C1(x) ⋅ y1 + C2(x) ⋅ y2. Производные неизвестных функции C1(x) и C2(x)определяются из системы уравнений , а сами функцииC1(x) и C2(x) получаются при последующем интегрировании.

Билет 13. Д. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Общее решение линейного однородного дифференциального уравнения с непрерывными на интервале интегрирования X коэффициентами определяется линейной комбинацией , где - линейно независимые частные решения ЛОДУ на X, а - произвольные постоянные.

Таким образом, общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид y0=C1⋅ y1+C2⋅ y2, где y1 и y2 – частные линейно независимые решения, а С1 и C2– произвольные постоянные.

Если принять частным решением ЛОДУ второго порядка с постоянными коэффициентами , то при подстановке этого решения в уравнение мы должны получить тождество:

Так мы получили так называемое характеристическое уравнение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами. Решения k1 и k2 этого характеристического уравнения определяют частные решения и нашего ЛОДУ второго порядка с постоянными коэффициентами.

В зависимости от коэффициентов p и q корни характеристического уравнения могут быть:

действительными и различными ,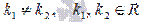

действительными и совпадающими ,

комплексно сопряженной парой .

Алгоритм нахождения общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами .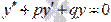

Записываем характеристическое уравнение k2 + p ⋅ k + q = 0.

Находим корни характеристического уравнения k1 и k2.

В зависимости от значений корней характеристического уравнения записываем общее решение ЛОДУ с постоянными коэффициентами в виде:

, если ;

, если ;

, если 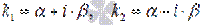.