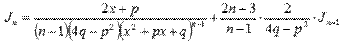Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Билет №4. Интегрирование дробно-рациональных функций.
|
|
Дробно-рациональная функция- функция вида «дробь», где и в числителе, и в знаменателе стоят многочлены в степени.

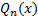 =
= 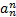 *
* 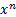 +
+ 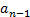 *
*  …
…

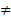 0 (самое старшее из слагаемых не должно быть равно нулю).
0 (самое старшее из слагаемых не должно быть равно нулю).
Первая теорема: если в дробно-рациональной функции степень многочлена в числителе больше степени многочлена в показателе, то нашу дробь можно записать в виде суммы
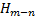 +
+ 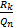 , где k< n
, где k< n
Первый шаг алгоритма: если m> n, тогда выполняем деление. Искомый интеграл равен интегралу от частного+ интеграл от дроби.
Вторая теорема: Любой многочлен в степени больше нуля равен произведению множителей вида ((x-a),  , (
, (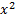 + px+ q),
+ px+ q), 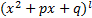 ) на
) на  , где L (степень)
, где L (степень)  2
2
Третья теорема: Если в
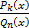 выполняется k< n, и знаменатель
выполняется k< n, и знаменатель 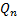 (x) записан как произведение множителей
(x) записан как произведение множителей
(x-a)*  * (
* (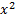 + px+ q)*
+ px+ q)* 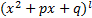 , то вся наша дробь
, то вся наша дробь 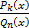 =
= 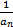 * сумма простейших дробей, где
* сумма простейших дробей, где  соответствует простейшей дроби вида
соответствует простейшей дроби вида 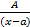 +
+  +…
+… 
Дроби  соответствует сумма дробей
соответствует сумма дробей 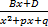 +
+ 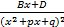 + …. До степени L.
+ …. До степени L.
Билет 5.Интегрирование простейших дробей первого типа 
Для решения этой задачи идеально подходит метод замены переменой

Интегрирование простейших дробей второго типа 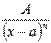
Для решения этой задачи также подходит метод непосредственного интегрирования:
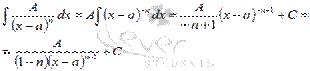
Интегрирование простейших дробей третьего типа 
Для начала представляем неопределенный интеграл 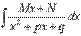 в виде суммы:
в виде суммы:
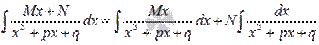
Первый интеграл берем методом подведения под знак дифференциала:
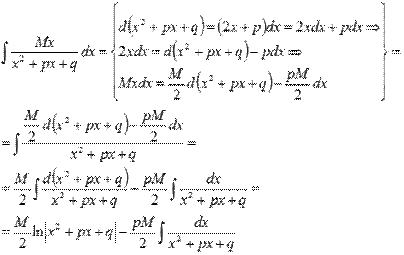
Поэтому,

Интегрирование простейших дробей четвертого типа 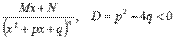
Первый шаг – подводим под знак дифференциала:
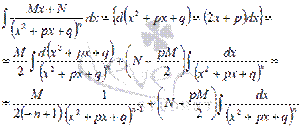
Второй шаг – нахождение интеграла вида 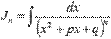 . Интегралы подобного вида находятся с использованием рекуррентных формул. Для нашего случая подходит следующая рекуррентная формула:
. Интегралы подобного вида находятся с использованием рекуррентных формул. Для нашего случая подходит следующая рекуррентная формула: