
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
БИЛЕТ 13Е Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
|
|
Общее решение на интервале X линейного неоднородного дифференциального уравнения 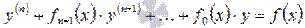 с непрерывными на интервале интегрирования X коэффициентами
с непрерывными на интервале интегрирования X коэффициентами  и непрерывной функцией f(x) равно сумме общего решения
и непрерывной функцией f(x) равно сумме общего решения  соответствующего ЛОДУ и какого-нибудь частного решения
соответствующего ЛОДУ и какого-нибудь частного решения  исходного неоднородного уравнения, то есть,
исходного неоднородного уравнения, то есть,  .
.
Существует несколько методов нахождения частного решения ЛНДУ второго порядка с постоянными коэффициентами. Методы выбираются в зависимости от вида функции f(x), стоящей в правой части уравнения.
1.Если f(x) является многочленом n-ой степени f(x) = Pn(x), то частное решение ЛНДУ ищется в виде  , где Qn(x) – многочлен степени n, а r – количество корней характеристического уравнения, равных нулю. Так как
, где Qn(x) – многочлен степени n, а r – количество корней характеристического уравнения, равных нулю. Так как  - частное решение уравнения
- частное решение уравнения  , то коэффициенты, определяющие многочлен Qn(x), находятся методом неопределенных коэффициентов из равенства
, то коэффициенты, определяющие многочлен Qn(x), находятся методом неопределенных коэффициентов из равенства  .
.
2.Если функция f(x) представлена произведением многочлена степени n и экспоненты  , то частное решение ЛНДУ второго порядка ищется в виде
, то частное решение ЛНДУ второго порядка ищется в виде  , где Qn(x) – многочлен n-ой степени, r – число корней характеристического уравнения, равных
, где Qn(x) – многочлен n-ой степени, r – число корней характеристического уравнения, равных  . Коэффициенты многочлена Qn(x) определяются из равенства
. Коэффициенты многочлена Qn(x) определяются из равенства  .
.
3.Если функция f(x) имеет вид  , где А1 и В1 – числа, то частное решение ЛНДУ представляется как
, где А1 и В1 – числа, то частное решение ЛНДУ представляется как  , гдеА и В – неопределенные коэффициенты, r – число комплексно сопряженных пар корней характеристического уравнения равных
, гдеА и В – неопределенные коэффициенты, r – число комплексно сопряженных пар корней характеристического уравнения равных  . Коэффициенты многочлена А и В находятся из равенства
. Коэффициенты многочлена А и В находятся из равенства  .
.
4.Если  , то
, то  , где r – число комплексно сопряженных пар корней характеристического уравнения, равных
, где r – число комплексно сопряженных пар корней характеристического уравнения, равных  , Pn(x), Qk(x), Lm(x) и Nm(x) - многочлены степени n, k, m и m соответственно, m = max(n, k). Коэффициенты многочленов Lm(x) и Nm(x) находятся из равенства
, Pn(x), Qk(x), Lm(x) и Nm(x) - многочлены степени n, k, m и m соответственно, m = max(n, k). Коэффициенты многочленов Lm(x) и Nm(x) находятся из равенства  .
.
5.Для любого другого вида функции f(x) применяется следующий алгоритм действий:
находится общее решение соответствующего линейного однородного уравнения как y0 = C1 ⋅ y1 + C2 ⋅ y2, где y1 и y2 - линейно независимые частные решения ЛОДУ, а С1 и С2 – произвольные постоянные;
варьируются произвольные постоянные, то есть, в качестве общего решения исходного ЛНДУ принимается y = C1(x) ⋅ y1 + C2(x) ⋅ y2;
производные функций C1(x) и С2(x) определяются из системы уравнений  , а сами функции C1(x) и C2(x)находятся при последующем интегрировании.
, а сами функции C1(x) и C2(x)находятся при последующем интегрировании.
БИЛЕТ №14
Система «хищник — жертва» — сложная экосистема, для которой реализованы долговременные отношения между видами хищника и жертвы, типичный пример коэволюции.
Отношения между хищниками и их жертвами развиваются циклически, являясь иллюстрацией нейтрального равновесия.
Биологическая система:
приспособления одних преодолеваются приспособлениями других. Длительное сосуществование формир. систему взаимодействий. Интродукция видов приводит к нарушениям в системе.
Математическая система:
x - кол-во жертв; y – кол-во хищников; t - время; α, β, γ, δ - коэффициенты, отражающие взаимосвязь видов:

1.) - Рассматр. сист. с достатком еды и отсутствием миграций видов:
 α = коэффициент прироста
α = коэффициент прироста
- Пока хищники не охотятся, они вымирают:
 γ = коэффициент убыли хищников
γ = коэффициент убыли хищников
- При их встречах (частота которых прямо пропорциональна величине  ):
):
 β = коэффициент убийств жертв, δ = коэффициент рождаемости хищников
β = коэффициент убийств жертв, δ = коэффициент рождаемости хищников
РЕШЕНИЕ:
Нахождение стационарной позиции системы.  Изменение численности популяции = 0.
Изменение численности популяции = 0.
 →
→ 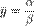


ЗАДАНИЕ ОТКЛОНЕНИЯ В СИСТ:
При внесении колебаний в систему  ,
,  , из-за их малой величины их
, из-за их малой величины их  2
2  3
3  n можно пренебречь:
n можно пренебречь:
Популяции x и y с малыми отклонениями:
 →
→
 →
→
Применяя их к уравнениям модели, следует:
 →
→ 
 →
→ 
При смещении данной системы из положения гармонического равновесия она испытывает действие возвращающей силы.