Билет 8. Свойства определенного интеграла.

Для функции y = f(x), определенной при x = a, справедливо равенство .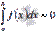

То есть, значение определенного интеграла с совпадающими пределами интегрирования равно нулю. Это свойство является следствием определения интеграла Римана, так как в этом случае каждая интегральная сумма для любого разбиения промежутка [a; a] и любого выбора точек равна нулю, так как , следовательно, пределом интегральных сумм является ноль.

Для интегрируемой на отрезке [a; b] функции выполняется .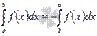

Другими словами, при перемене верхнего и нижнего пределов интегрирования местами значение определенного интеграла меняется на противоположное. Это свойство определенного интеграла также следует из понятия интеграла Римана, только нумерацию разбиения отрезка следует начинать с точки x = b.

для интегрируемых на отрезке [a; b] функций y = f(x) и y = g(x).

Доказательство.

Запишем интегральную сумму функции 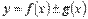для данного разбиения отрезка и данного выбора точек :

где и 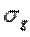- интегральные суммы функций y = f(x) и y = g(x) для данного разбиения отрезка соответственно.

Переходя к пределу при получим , что по определению интеграла Римана равносильно утверждению доказываемого свойства.

Постоянный множитель можно выносить за знак определенного интеграла. То есть, для интегрируемой на отрезке [a; b] функции y = f(x) и произвольного числа k справедливо равенство .

Доказательство этого свойства определенного интеграла абсолютно схоже с предыдущим:

Пусть функция y = f(x) интегрируема на интервале X, причем и 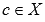, тогда .

Это свойство справедливо как для , так и для или .

Доказательство можно провести, опираясь на предыдущие свойства определенного интеграла.

Если функция интегрируема на отрезке [a; b], то она интегрируема и на любом внутреннем отрезке .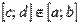

Доказательство основано на свойстве сумм Дарбу: если к имеющемуся разбиению отрезка добавить новые точки, то нижняя сумма Дарбу не уменьшится, а верхняя – не увеличиться.

Если функция y = f(x) интегрируема на отрезке [a; b] и 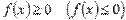для любого значения аргумента 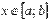, то .

Это свойство доказывается через определение интеграла Римана: любая интегральная сумма для любого выбора точек разбиения отрезка и точек при будет неотрицательной (не положительной).

Следствие.

Для интегрируемых на отрезке [a; b] функций y = f(x) и y = g(x) справедливы неравенства:

Это утверждение означает, что допустимо интегрирование неравенств. Этим следствием мы будем пользоваться при доказательстве следующих свойств.

Пусть функция y = f(x) интегрируема на отрезке [a; b], тогда справедливо неравенство .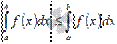

Доказательство.

Очевидно, что . В предыдущем свойстве мы выяснили, что неравенство можно почленно интегрировать, поэтому, справедливо . Это двойное неравенство можно записать как .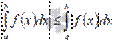

Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке [a; b] и 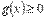для любого значения аргумента , тогда , где и .

Доказательство проводится аналогично. Так как m и M – наименьшее и наибольшее значение функции y = f(x) на отрезке [a; b], то . Домножение двойного неравенства на неотрицательную функцию y = g(x) приводит нас к следующему двойному неравенству 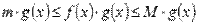. Интегрируя его на отрезке [a; b], придем к доказываемому утверждению.

Следствие.

Если взять g(x) = 1, то неравенство примет вид .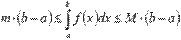

Первая формула среднего значения.

Пусть функция y = f(x) интегрируема на отрезке [a; b], и , тогда существует такое число , что .

Следствие.

Если функция y = f(x) непрерывна на отрезке [a; b], то найдется такое число , что .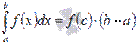

Первая формула среднего значения в обобщенной форме.

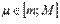Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке [a; b], и , а g(x) > 0 для любого значения аргумента . Тогда существует такое число , что .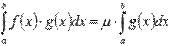

Вторая формула среднего значения.

Если на отрезке [a; b] функция y = f(x) интегрируема, а y = g(x) монотонна, то существует такое число , что справедливо равенство 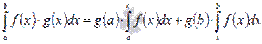.