
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Скалярное произведение
|
|
[править]
Материал из Википедии — свободной энциклопедии
Скаля́ рное произведе́ ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.
Обычно используется одно из следующих обозначений:
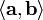 ,
,
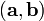 ,
,
 ,
,
или (обозначение Дирака, часто применяемое в квантовой механике для векторов состояния):
 .
.
Обычно предполагается что скалярное произведение положительно определено, то есть
 для всех
для всех  .
.
Если этого не предполагать, то произведение называется индефинитным.
Определение
Скалярным произведением в векторном пространстве  над полем
над полем  называется функция
называется функция  для элементов
для элементов  , принимающая значения в
, принимающая значения в  , определенная для каждой пары элементов и удовлетворяющая следующим условиям:
, определенная для каждой пары элементов и удовлетворяющая следующим условиям:
для любых трех элементов  и
и 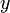 пространства
пространства  и любых чисел
и любых чисел  справедливо равенство
справедливо равенство  (линейность скалярного произведения по первому аргументу);
(линейность скалярного произведения по первому аргументу);
для любых 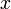 и
и 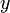 справедливо равенство
справедливо равенство  , где черта означает комплексное сопряжение (эрмитова симметричность);
, где черта означает комплексное сопряжение (эрмитова симметричность);
для любого 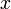 имеем
имеем  , причем
, причем  только при
только при  (положительная определенность скалярного произведения).
(положительная определенность скалярного произведения).
Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.
Заметим, что из п.2 определения следует, что  действительное. Поэтому п.3 имеет смысл несмотря на комплексные (в общем случае) значения скалярного произведения.
действительное. Поэтому п.3 имеет смысл несмотря на комплексные (в общем случае) значения скалярного произведения.
[править]Элементарное определение


A • B = | A | | B | cos(θ)
Элементарное определение скалярного произведения используется, когда определения длины вектора и угла между векторами введены независимым образом до введения понятия скалярного произведения (как правило, так и поступают при изложении элементарной геометрии). В этом случае скалярное произведение определяется через длины сомножителей и угол между ними:

Современная аксиоматика обычно строится начиная со скалярного произведения, и тогда длина вектора и угол определяются уже через скалярное произведение (см. ниже).
[править]Связанные определения
В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия:
Длина вектора, под которой понимается уже упомянутая выше его евклидова норма:  (термин 'длина' обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).
(термин 'длина' обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).
Углом между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):

В случае, если пространство является псевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):
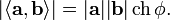
Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Например, ортогональные многочлены на самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.
Пространство (вещественное или комплексное) с положительно определённым скалярным произведением называется предгильбертовым пространством.
При этом конечномерное вещественное пространство с положительно определённым скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.
Случай, когда скалярное произведение не является знакоопределённым, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называется псевдоевклидовым (важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.
[править]Примеры
В трёхмерном вещественном векторном пространстве векторов  введение скалярного произведения по формуле
введение скалярного произведения по формуле  превращает это пространство в евклидово пространство. Аналогичное утверждение верно для евклидова пространства любой размерности (в сумму тогда входит количество членов, равное размерности пространства).
превращает это пространство в евклидово пространство. Аналогичное утверждение верно для евклидова пространства любой размерности (в сумму тогда входит количество членов, равное размерности пространства).
В любом евклидовом пространстве (размерности n) всегда можно выбрать[1] ортонормированный базис 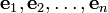
при разложении векторов по которому:
 ,
,
 итд,
итд,
скалярное произведение будет выражаться приведенной выше формулой:
 .
.
В таком же, но комплексном, пространстве, скалярное произведение вводится по несколько другой формуле:  . Здесь через
. Здесь через  обозначено число, комплексно сопряжённое к
обозначено число, комплексно сопряжённое к  . При таком определении скалярное произведение становится положительно определённым. Без комплексного сопряжения аксиома эрмитовости скалярного произведения была бы нарушена, а значит, вещественности определённой через него нормы вектора добиться бы не удалось, то есть норма в обычном смысле им бы не порождалась.
. При таком определении скалярное произведение становится положительно определённым. Без комплексного сопряжения аксиома эрмитовости скалярного произведения была бы нарушена, а значит, вещественности определённой через него нормы вектора добиться бы не удалось, то есть норма в обычном смысле им бы не порождалась.
В пространстве измеримых интегрируемых с квадратами на некоторой области Ω вещественных функций можно ввести положительно определённое скалярное произведение:

В аналогичном случае для комплексных функций, если требуется эрмитовость (и положительная определённость) скалярного произведения, надо добавить комплексное сопряжение к f или g под интегралом.
При использовании неортонормированных базисов скалярное произведение выражается через компоненты векторов с участием метрического тензора gij:

при этом сама метрика (говоря точнее, ее представление в данном базисе) так связана со скалярными произведениями базисных векторов  :
:
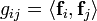
(метрика в ортонормированных базисах тривиальна, то есть представлена единичной матрицей gij = δ ij)
Аналогичные конструкции скалярного произведения можно вводить и на бесконечномерных пространствах, например, на пространствах функций:
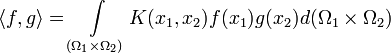
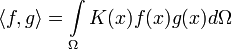
где К — положительно определённая, в первом случае симметричная относительно перестановки аргументов (при комплексных x — эрмитова) функция (если нужно иметь обычное симметричное положительно определённое скалярное произведение).
[править]Неравенство Коши — Буняковского
Для любых элементов  и
и  линейного пространства со скалярным произведением выполняется неравенство [1]
линейного пространства со скалярным произведением выполняется неравенство [1]

[править]Применение
Использование скалярного произведения крайне широко, как в элементарных, так и в весьма абстрактных областях математики, физики и прикладных наук.
Широко известны следующие применения:
Любые геометрические вычисления (как собственно в математике, так и в приложениях), связанные с длинами, углами, проецированием, ортогональностью.
Например, теорема косинусов легко выводится с использованием скалярного произведения:

Угол между векторами:

Оценка угла между векторами:
в формуле  знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.
знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.
Проекция вектора 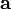 на направление, определяемое единичным вектором
на направление, определяемое единичным вектором  :
:
 ,
,
условие ортогональности[2] (перпендикулярности) векторов 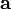 и
и 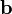 :
:

итд.
(При этом технические возможности вычислений со скалярными произведениями, как и вообще с векторами, значительно возрастают, если использовать — при желании или необходимости — и компонентное представление векторов вкупе с компонентным выражением скалярного произведения).
Площадь также выражается через скалярное произведение, например, двумерная площадь параллелограмма, натянутого на два вектора 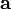 и
и 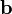 , равна
, равна
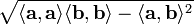
Аналогичные вычисления в геометризованных теориях в физике (таких, как СТО или ОТО).
Разложение векторов по базису и переход к новому базису, являющееся основой многих разделов математики и ключевым приемом эффективного решения практических геометрических задач или практических задач, формулируемых на языке линейной алгебры (относящихся, например, к статистике).
В том числе, в бесконечномерном случае: ряды Фурье, преобразования Фурье.
В векторном анализе — вычисление контурных интегралов, потоков, применение с оператором набла.
[править]Обобщения
Простейшим обобщением конечномерного скалярного произведения в тензорной алгебре является свёртка по повторяющимся индексам. Аналогичное обобщение в принципе нетрудно сделать и в бесконечномерном случае (Для бесконечномерных пространств функций — см. примеры (выше)).
[править]Примечания
↑ Ортонормированность базиса определяется условием

заключающемся в равенстве нулю скалярных произведений разных базисных векторов, например, первого и второго, первого и третьего, итд (ортогональность), и равенстве единице — скалярного произведения каждого базисного вектора с самим собой (нормированность). Упоминаемые в основном тексте формулы получаются прямым перемножением векторов, разложенных по такому базису, учитывая свойства скалярного произведения, особенно его билинейность, позволяющую раскрывать скобки итп как при вычислениях с обычными числами.
↑ В абстрактной формулировке названное условие  — это всего лишь определение ортогональности. Аналогично, две формулы выше в абстрактной формулировке также являются просто определениями соответствующих понятий через скалярное произведение, но они все могут с успехом быть использованы в конкретных вычислениях, например, в элементарной геометрии, независимо от того, какая система определений используется, современная абстрактная или традиционная элементарная.
— это всего лишь определение ортогональности. Аналогично, две формулы выше в абстрактной формулировке также являются просто определениями соответствующих понятий через скалярное произведение, но они все могут с успехом быть использованы в конкретных вычислениях, например, в элементарной геометрии, независимо от того, какая система определений используется, современная абстрактная или традиционная элементарная.