Свойства скалярного произведения

1. Скалярное произведение обладает переместительным свойством: ab=ba

1. Скалярное произведение двух векторов подчиняется коммутативному закону, т.е. для любых векторов и .

Очевидно, из определения скалярного произведения:

.

2. Для любого числа λ и любых векторов имеем:

.

Доказательство. Ограничимся случаем, когда λ > 0. В этом случае угол между векторами и совпадает с углом между векторами и , .

Поэтому . Откуда

Аналогично доказывается и равенство .

Случай λ < 0 рассмотреть самостоятельно.

3. Для любых векторов 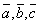выполняется равенство .

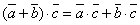Доказательство. Используя определение скалярного произведения и свойства проекций вектора на ось, будем иметь

4. Для любого вектора выполняется соотношение .

Действительно, так как , то .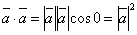

Из этого свойства в частности следует .

5. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда равен нулю один из сомножителей или векторы перпендикулярны.

Это свойство очевидно из определения скалярного произведения.

Таким образом, необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.