
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства
|
|
[править]Геометрические свойства векторного произведения


Рисунок 1: Площадь параллелограмма равна векторному произведению.


Рисунок 2: Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на a × b и вектора a на b × c, первым шагом является нахождение скалярных произведений.
§ Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
§ Модуль векторного произведения  равняется площади S параллелограмма, построенного на приведённых к общему началу векторах
равняется площади S параллелограмма, построенного на приведённых к общему началу векторах 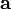 и
и 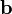 (см. Рисунок 1)
(см. Рисунок 1)
§ Если  — единичный вектор, ортогональный векторам
— единичный вектор, ортогональный векторам 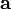 и
и 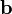 и выбранный так, что тройка
и выбранный так, что тройка 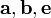 — правая, а S — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
— правая, а S — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:

§ Если  — какой-нибудь вектор, π — любая плоскость, содержащая этот вектор,
— какой-нибудь вектор, π — любая плоскость, содержащая этот вектор,  — единичный вектор, лежащий в плоскости π и ортогональный к
— единичный вектор, лежащий в плоскости π и ортогональный к  ,
,  — единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов
— единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов  является правой, то для любого лежащего в плоскости π вектора
является правой, то для любого лежащего в плоскости π вектора 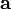 справедлива формула
справедлива формула

§ При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.

На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:

Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0, если векторы параллельны.
[править]Алгебраические свойства векторного произведения
| Представление | Описание |

| свойство антикоммутативности |

| свойство ассоциативности относительно умножения на скаляр |

| свойство дистрибутивности по сложению |
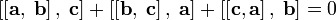
| тождество Якоби, выполняется в  и нарушается в и нарушается в 
|

| |
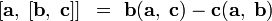
| формула «БАЦ минус ЦАБ», тождество Лагранжа |

| Это частный случай мультипликативности 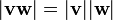 нормы кватернионов нормы кватернионов
|

| значение этого выражения называют смешанным произведением векторов a, b, c и обозначают  либо либо 
|
Условия параллельности и перпендикулярности векторов
Так как скалярное произведение двух перпендикулярных векторов  и
и  равно 0, то условием перпендикулярности отличных от нуля векторов будет равенство
равно 0, то условием перпендикулярности отличных от нуля векторов будет равенство  .
.
При умножении вектора  на скаляр
на скаляр  получаем вектор
получаем вектор 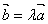 одного направления с
одного направления с  при λ > 0и противоположного направления при λ < 0. Но всегда векторы
при λ > 0и противоположного направления при λ < 0. Но всегда векторы  будут параллельны.
будут параллельны.
Поэтому условием параллельности векторов  будет пропорциональность их соответствующих координат:
будет пропорциональность их соответствующих координат: 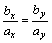 .
.
3)
1.16. Смешанное произведение векторов и его свойства
Смешанным произведением векторов  называется число
называется число  , равное скалярному произведению вектора
, равное скалярному произведению вектора  на векторное произведение векторов
на векторное произведение векторов 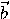 и
и  . Смешанное произведение обозначается
. Смешанное произведение обозначается  .
.
Геометрические свойства смешанного произведения
1. Модуль смешанного произведения некомпланарных векторов  равен объему
равен объему  параллелепипеда, построенного на этих векторах. Произведение
параллелепипеда, построенного на этих векторах. Произведение  положительно, если тройка векторов
положительно, если тройка векторов  — правая, и отрицательно, если тройка
— правая, и отрицательно, если тройка  — левая, и наоборот.
— левая, и наоборот.
2. Смешанное произведение  равно нулю тогда и только тогда, когда векторы
равно нулю тогда и только тогда, когда векторы  компланарны:
компланарны:
 векторы
векторы  компланарны.
компланарны.
Докажем первое свойство. Найдем по определению смешанное произведение:, где 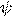 — угол между векторами
— угол между векторами  и
и 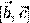 . Модуль векторного произведения (по геометрическому свойству 1) равен площади
. Модуль векторного произведения (по геометрическому свойству 1) равен площади  параллелограмма, построенного на векторах
параллелограмма, построенного на векторах 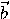 и
и  :. Поэтому
:. Поэтому 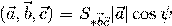 . Алгебраическое значение
. Алгебраическое значение  длины проекции вектора
длины проекции вектора  на ось, задаваемую вектором
на ось, задаваемую вектором 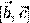 , равно по модулю высоте
, равно по модулю высоте 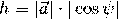 параллелепипеда, построенного на векторах
параллелепипеда, построенного на векторах  (рис. 1.47). Поэтому модуль смешанного произведения равен объему
(рис. 1.47). Поэтому модуль смешанного произведения равен объему  этого параллелепипеда:
этого параллелепипеда:

Знак смешанного произведения определяется знаком косинуса угла 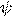 . Если тройка
. Если тройка  правая, то
правая, то  и смешанное произведение
и смешанное произведение  положительно. Если же тройка
положительно. Если же тройка  левая, то
левая, то 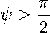 и смешанное произведение
и смешанное произведение  отрицательно.
отрицательно.
Докажем второе свойство. Равенство возможно в трех случаях:  или
или 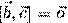 (т.е.
(т.е. 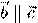 ), или
), или  (т.е. вектор
(т.е. вектор  принадлежит плоскости векторов
принадлежит плоскости векторов 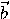 и
и  ). В каждом случае векторы
). В каждом случае векторы  компланарны (см. разд. 1.1).
компланарны (см. разд. 1.1).
Алгебраические свойства смешанного произведения
1. При перестановке двух множителей смешанное произведение изменяет знак на противоположный:
При циклической (круговой) перестановке множителей смешанное произведение не изменяется:
2. Смешанное произведение линейно по любому множителю.
Первое свойство следует из геометрического свойства 1 и свойств ориентации троек векторов (см. разд. 1.9), поскольку от перестановки двух множителей модуль смешанного произведения не изменяется, а меняется только ориентация тройки. При циклической перестановке векторов ориентация тройки не изменяется.
Второе свойство следует из линейности скалярного произведения и свойства 1.
Пример 1.21. Объем параллелепипеда, построенного на векторах  , равен
, равен  . Найти объем параллелепипеда, построенного на векторах.
. Найти объем параллелепипеда, построенного на векторах.
Решение. Используя алгебраические и геометрические свойства, найдем смешанное произведение
а затем его модуль  . По первому геометрическому свойству смешанного произведения искомый объем равен
. По первому геометрическому свойству смешанного произведения искомый объем равен  .
.
Теорема 1.9 (формула вычисления смешанного произведения). Если векторы  в правом ортонормированном базисе
в правом ортонормированном базисе 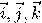 имеют координаты
имеют координаты  ;
;  ;
;  соответственно, то смешанное произведение этих векторов находится по формуле
соответственно, то смешанное произведение этих векторов находится по формуле
В самом деле, учитывая (1.10) и (1.15), по определению находим:
что и требовалось доказать.
4)