Операции над комплексными числами. Деление комплексных чисел

Последняя операция которую осталось рассмотреть — операция деления комплексных чисел. Рассмотрим деление в показательной форме:

(23)

Таким образом при делении комплексных чисел их модули делятся а фазы вычитаются. При делении необходимо чтобы . Получим формулу для деления комплексных чисел в явной форме. Пусть

(24)

умножим и числитель и знаменатель дроби на число комплексно-сопряженное знаменателя:

.

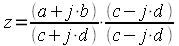(25)

Исходя из (22) в знаменателе дроби получим квадрат модуля знаменателя а числитель перемножим по правилу умножения комплексных чисел:

.

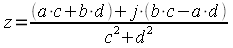(26)

Поделив почленно реальную и мнимую часть числителя на знаменатель получим:

.

(27)

Выражение (27) - формула деления комплексных чисел в явной форме. Как можно заметить операции сложения и вычитания удобнее выполнять в явном виде, тогда как умножать и делить комплексные числа быстрее и легче в показательной форме.

6)РЕШЕНИЕ УРАВНЕНИЯ .