Ограниченные последовательности. Теорема о том, что последовательность, имеющая предел, обязана быть ограниченной.

Ограниченная сверху последовательность — это последовательность элементов множества X, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности.

(x_n) ограниченная сверху

Ограниченная снизу последовательность — это последовательность элементов множества X, для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.

(x_n) ограниченная снизу

Ограниченная последовательность (ограниченная с обеих сторон последовательность) — это последовательность, ограниченная и сверху, и снизу.

(x_n) ограниченная

Неограниченная последовательность — это последовательность, которая не является ограниченной.

(x_n) неограниченная

Критерий ограниченности числовой последовательности:

Числовая последовательность является ограниченной тогда и только тогда, когда существует такое число, что модули всех членов последовательности не превышают его.

(x_n) ограниченная

Теорема: если последовательность имеет предел, то она обязана быть ограниченной.

Дано: 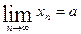1) Воспользуемся определением предела для ε =1

Доказать: 2) Найдем для него подходящее N, т.е. такое N, что

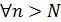|x_n- a|< 1 a–1 < x_n< a+1

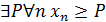3) M = max (a+1, x_n n ≤ N)

4) P = min (a-1, x_n n ≤ N)