Односторонние пределы функции. Классификация точек разрыва. Пример.

Определение: Если f(x) ®A₁при х ® а только при x< a, то - называется пределом функции f(x) в точке х = а слева, а еслиf(x) ®A₂при х ® а только при x> a, то 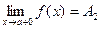называется пределом функции f(x) в точке х = а справа.

у

f(x)

А₂

А₁

Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы А₁ и А₂ называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x).

Точки разрыва и их классификация.

Определение. Если функция f(x) определена в некоторой окрестности точки х₀, но не является непрерывной в самой точке х₀, то она называется разрывной функцией, а точка х₀ – точкой разрыва.

Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х₀, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х₀ является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Определение. Точка х₀ называется точкой разрыва функции f(x), если f(x) не определена в точке х₀ или не является непрерывной в этой точке.

Определение. Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х₀, достаточно того, что она определена слева и справа от нее.

Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.

Определение. Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)

не является непрерывной в любой точке х₀.

Пример. Функция f(x) = имеет в точке х₀ = 0 точку разрыва 2 – го рода, т.к.

.

Пример. f(x) =

Функция не определена в точке х = 0, но имеет в ней конечный предел , т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:

График этой функции:

17. Функции, непрерывные на отрезке. Их свойства: ограниченность, достижение наибольшего и наименьшего значений. Пример, показывающий существенность условия «на отрезке».

Функция f(х) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке этого интервала (отрезка). При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.

Свойства функций, непрерывных на отрезке:

Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M ≤ f(x) ≤ M.

Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения (рис. 7.4). Т.е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причемm ≤ f(x) ≤ M.

Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.

Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b] и принимает на его концах неравные значения f(a) = A, f(b) = B, то на этом отрезке она принимает и все промежуточные значения между А и В.

Геометрически свойство очевидно (см. рис.8.4)

Для любого числа С, заключенного между А и В, найдется точка свнутри этого отрезка такая, что f(с)=C. Прямая у=С пересечет график функции по крайней мере в одной точке.

Свойство 4: Если функция f(x) непрерывна в точке х = х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.

Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x) – непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0 (см. рис. 9.4).

Т.е. если sign(f(a)) ≠ sign(f(b)), тох0: f(x0) = 0.