Определение одностороннего бесконечного предела. Пример.

Пусть числовая функция 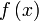задана на множестве , в котором для любого числа 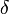найдётся элемент, лежащий правее него. В этом случае число 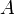называется пределом функции 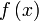на плюс бесконечности, если для произвольного положительного числа отыщется отвечающее ему положительное число 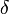такое, что для всех точек, лежащих правее 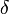, справедливо неравенство .

Пусть числовая функция 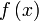задана на множестве , в котором для любого числа 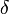найдётся элемент, лежащий левее него. В этом случае число 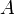называется пределом функции 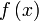на минус бесконечности, если для произвольного положительного числа отыщется отвечающее ему положительное число 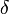такое, что для всех точек, лежащих левее , справедливо неравенство .

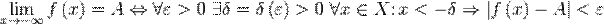
Первый замечательный предел. Пример.

Второй замечательный предел. Пример.

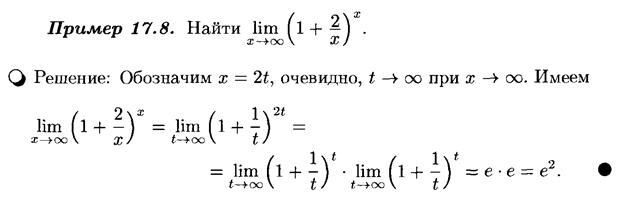
Понятие непрерывной функции. Непрерывность слева, непрерывность справа.

Пусть функция у = f (х) определена в некотором интервале, а их — два произвольных значения аргумента из этого интервала.

Положим

, откуда .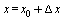
Говорят, что для перехода от значения аргумента к значению х первоначальному значению придано приращение Δ х. Приращением Δ y функции у = f (х), соответствующим приращению Δ х аргумента х в точке , называется разность .
Функция у = f (х) называется непрерывной в точке , если бесконечно малому приращению Δ х аргумента х в точке соответствует бесконечно малое приращение функции Δ y, т. е. 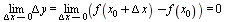. Другими словами, функция у = f (х) непрерывна в точке , если
, т. е. предел функции в точке равен значению функции в этой точке.
Функция, непрерывная в каждой точке интервала, называется непрерывной на этом интервале.
Пример 1. Функция у = х непрерывна при любом значении .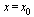
В самом деле,
, и значит,

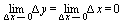
Пример 2. Функция у = sin х непрерывна при любом значении .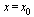
В самом деле, 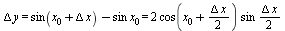Отсюда

, так как

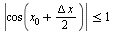, a

Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.

Если односторонний предел , то функция называется непрерывной справа. Если односторонний предел (см. выше) , то функция называется непрерывной слева.