
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Число е как предел последовательности.
|
|
Число e выражается через предел следующим образом:

Это число является трансцендентным и приблизительно равно 2, 718281828... Выполнив подстановку  , где
, где  , получим альтернативную формулу для данного предела:
, получим альтернативную формулу для данного предела:

Здесь мы имеем дело со степенными выражениями, когда и основание и степень стремятся к числу a (или к бесконечности). Во многих случаях такие пределы удобно вычислять, предварительно логарифмируя функцию под знаком предела.
Вычислить предел  .
.
Решение.
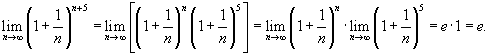
Бесконечно малые и бесконечно большие последовательности, связь между ними. Доказать, что величины, обратные к членам бесконечно большой последовательности, составляют бесконечно малую последовательность.
Последовательность {α n} называется бесконечно малой, если 
Теорема 1: Сумма бесконечно малых последовательностей является бесконечно малой.
Теорема 2: Произведение бесконечно малой последовательности на ограниченную является бесконечно малым.
Последовательность {β n} называется бесконечно большой, если для любого М > 0 существует такое N, что при любом n > N |β n| > M
( )
)
Теорема: Величины, обратные к членам бесконечно большой последовательности, составляют бесконечно малую последовательность.
 Дано:
Дано:
{β n} – бесконечно большая 
последовательность Возьмем произвольное ε > 0 и воспользуемся
 Доказать: определением бесконечно большой послед.:
Доказать: определением бесконечно большой послед.:
 - бесконечно малая
- бесконечно малая 
последовательность
8.  Теорема о действиях над пределами последовательностей. Пример ее применения.
Теорема о действиях над пределами последовательностей. Пример ее применения.

