
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема Лапласа
|
|
Теорема 1. (Теорема Лапласа) Зафиксируем в квадратной матрице 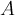 произвольные
произвольные 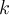 строк с номерами
строк с номерами  . Тогда определитель матрицы
. Тогда определитель матрицы 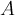 равен сумме произведений всевозможных миноров, построенных на этих строках, на их алгебраическое дополнение. То есть
равен сумме произведений всевозможных миноров, построенных на этих строках, на их алгебраическое дополнение. То есть  .
.
Если зафиксировать в матрице только одну строку с номером  , то, как частный случай из теоремы Лапласа, получим следующую формулу:
, то, как частный случай из теоремы Лапласа, получим следующую формулу:
 .
.
Пример 6. Вычислим определитель матрицы 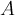 из примера 3 с помощью разложения по первой строке:
из примера 3 с помощью разложения по первой строке:

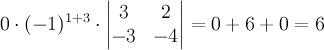 .
.
17)
Свойства определителей матриц:
Свойство № 1:
Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование).
|А| = |А|Т

Следствие:
Столбцы и строки определителя матрицы равноправны, следовательно, свойства присущие строкам выполняются и для столбцов.
Свойство № 2:
При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:

Свойство № 3:
Определитель матрицы, имеющий два одинаковых ряда, равен нулю.

Свойство № 4:
Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.
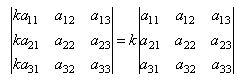
Следствия из свойств № 3 и № 4:
Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.
Свойство № 5:
Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю.
Свойство № 6:
Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-х определителей по формуле:

Свойство № 7:
Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.

Пример применения свойств для вычисления определителя матрицы:
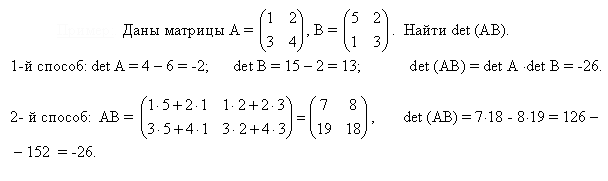
18)
19)
Метод Крамера — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы.
Пусть имеется система уравнений:
 .
.
Обозначим через Δ определитель матрицы системы и через Δ j определитель, который получается из определителя Δ заметой j-го столбца столбцом правых частей системы (j=1, 2,...n):
 .
.
Теорема
Если определитель матрицы отличен от нуля, т.е. Δ ≠ 0, то система имеет единственное решение, которое находится по формуле:
 .
.
20)
ЛИНЕЙНОЕ ПРОСТРАНСТВО.
Множество M элементов u, v, w,... произвольной природы, в котором определены операции сложения и умножения на число, подчиняющиеся определенным аксиомам, называется линейным пространством.
Пусть M - множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число:
паре элементов множества  ,
,  отвечает элемент
отвечает элемент  , называемый суммой
, называемый суммой 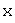 и
и  .
.
Паре  ,
,  отвечает элемент
отвечает элемент  , называемый произведением числа
, называемый произведением числа  и элемента
и элемента 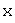 .
.
Будем называть множество М линейным пространством, если для всех его элементов определены операции сложения и умножения на действительное число и для любых элементов  и произвольных чисел
и произвольных чисел  справедливо:
справедливо:
1) 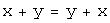 (сложение коммутативно).
(сложение коммутативно).
2) 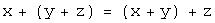 (сложение ассоциативно).
(сложение ассоциативно).
3) существует единственный нулевой элемент  такой, что
такой, что  ,
, 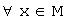 .
.
4) для каждого элемента существует единственный противоположный элемент  такой, что
такой, что  ,
, 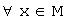 .
.
5)  (умножение на число ассоциативно).
(умножение на число ассоциативно).
6) 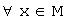 .
.
7)  (умножение на число дистрибутивно относительно сложения элементов).
(умножение на число дистрибутивно относительно сложения элементов).
8)  (умножение вектора на число дистрибутивно относительно сложения чисел).
(умножение вектора на число дистрибутивно относительно сложения чисел).
ВСЁ ЭТО АКСИОМЫ ЛИНЕЙНОГО ПРОСТРАНСТВА (1-8).
Линейное пространство часто называют векторным пространством, а его элементы - векторами.
Базис и размерность линейного пространства. Координаты вектора в заданном базисе.
Говорят, что вектор линейного пространства линейно выражается через векторы  если его можно представить в виде линейной комбинации этих элементов, т.е. представить в виде
если его можно представить в виде линейной комбинации этих элементов, т.е. представить в виде  .
.
Если любой вектор системы 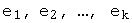 векторов линейного пространства
векторов линейного пространства  линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой. Система векторов, которая не является линейно зависимой, называется линейно независимой.
линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой. Система векторов, которая не является линейно зависимой, называется линейно независимой.
Справедливо следующее утверждение:
Система 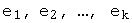 векторов линейного пространства
векторов линейного пространства  линейно независима тогда и только тогда, когда из равенства
линейно независима тогда и только тогда, когда из равенства 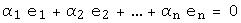 следует равенство нулю всех коэффициентов
следует равенство нулю всех коэффициентов 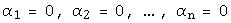 .
.
Если в линейном пространстве  существует линейно независимая система из n векторов, а любая система из (n+1)-го вектора линейно зависима, то число n называется размерностью пространства
существует линейно независимая система из n векторов, а любая система из (n+1)-го вектора линейно зависима, то число n называется размерностью пространства  . В этом случае пространство
. В этом случае пространство  называют n-мерным линейным пространством или n-мерным векторным пространством.
называют n-мерным линейным пространством или n-мерным векторным пространством.
Любая упорядоченная линейно независимая система n векторов  линейного пространства
линейного пространства  образует базис пространства и любой вектор
образует базис пространства и любой вектор 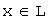 единственным образом выражается через векторы базиса:
единственным образом выражается через векторы базиса: 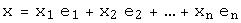 .
.
Числа  называют координатами вектора
называют координатами вектора 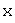 в базисе
в базисе  и обозначают
и обозначают 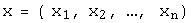 .При этом для любых двух произвольных векторов n-мерного линейного пространства
.При этом для любых двух произвольных векторов n-мерного линейного пространства 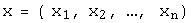 ,
, 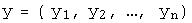 и произвольного числа
и произвольного числа  справедливо:
справедливо:  и
и 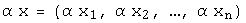 .Это означает, что все n-мерные линейные пространства “устроены” одинаково как пространство
.Это означает, что все n-мерные линейные пространства “устроены” одинаково как пространство  векторов-столбцов из n действительных чисел, т.е. что все они изоморфны пространству
векторов-столбцов из n действительных чисел, т.е. что все они изоморфны пространству  . Линейные пространства
. Линейные пространства  и
и 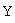 называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что если векторам
называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что если векторам 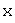 и
и 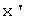 из
из  соответствуют векторы
соответствуют векторы  и
и  из
из 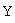 , то вектору
, то вектору  соответствует вектор
соответствует вектор  и при любом
и при любом  вектору
вектору  соответствует вектор
соответствует вектор  .
.
Изоморфизм n-мерных линейных пространств пространству  означает, что соотношения между элементами n-мерного линейного пространства и операции с ними можно изучать как соотношения между векторами из
означает, что соотношения между элементами n-мерного линейного пространства и операции с ними можно изучать как соотношения между векторами из  и операции с ними и что всякое утверждение относительно векторов из
и операции с ними и что всякое утверждение относительно векторов из  справедливо для соответствующих элементов любого n-мерного линейного пространства.
справедливо для соответствующих элементов любого n-мерного линейного пространства.
Например, доказано, что система векторов  из
из 
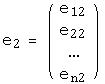 ,
, 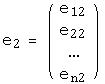 ,..
,.. 
образует базис в  тогда и только тогда, когда отличен от нуля определитель матрицы, со столбцами
тогда и только тогда, когда отличен от нуля определитель матрицы, со столбцами  :
:
 .
.
Для векторов  из
из  это означает, что они образуют базис в
это означает, что они образуют базис в  тогда и только тогда, когда отличен от нуля определитель матрицы, столбцами которой являются компоненты векторов
тогда и только тогда, когда отличен от нуля определитель матрицы, столбцами которой являются компоненты векторов  .
.
Пусть  и
и  - два базиса в
- два базиса в  . Матрицей перехода от базиса
. Матрицей перехода от базиса  к базису
к базису  называется матрица С, столбцами которой являются координаты векторов
называется матрица С, столбцами которой являются координаты векторов  в базисе
в базисе  :
:
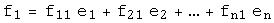
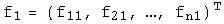


…
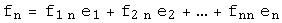
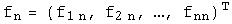
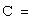
 ,
,  .
.
Вектор 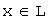 линейно выражается через векторы обоих базисов. Тогда, если
линейно выражается через векторы обоих базисов. Тогда, если 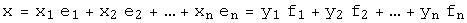 , то координаты вектора
, то координаты вектора 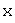 в базисе
в базисе  , и его координаты в базисе
, и его координаты в базисе  связаны соотношениями
связаны соотношениями
 .
.
21)
Линейная зависимость и линейная независимость строк (столбцов) матрицы.
Столбец 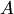 называется линейной комбинацией столбцов
называется линейной комбинацией столбцов  одинаковых размеров, если
одинаковых размеров, если 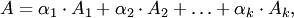 где
где  — некоторые числа. В этом случае говорят, что столбец
— некоторые числа. В этом случае говорят, что столбец 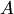 разложен по столбцам
разложен по столбцам  , а числа
, а числа  называют коэффициентами разложения. Линейная комбинация
называют коэффициентами разложения. Линейная комбинация 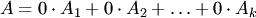 с нулевыми коэффициентами называется тривиальной.
с нулевыми коэффициентами называется тривиальной.
Если столбцы имеют вид
 ,
,
то матричному равенству соответствуют поэлементные равенства

Аналогично формулируется определение линейной комбинации строк.
Набор столбцов  одинаковых размеров называется системой столбцов.
одинаковых размеров называется системой столбцов.
Система из 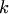 столбцов
столбцов  называется линейно зависимой, если существуют такие числа
называется линейно зависимой, если существуют такие числа  , не все равные нулю одновременно, что
, не все равные нулю одновременно, что  . (3.2)
. (3.2)
Здесь ‘о’ обозначается нулевой столбец соответствующих размеров.
Система из 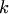 столбцов
столбцов  называется линейно независимой, если равенство (3.2) возможно только при
называется линейно независимой, если равенство (3.2) возможно только при  , т.е. когда линейная комбинация в левой части тривиальная.
, т.е. когда линейная комбинация в левой части тривиальная.
Любая часть системы столбцов называется подсистемой.
Пример. Используя определение, установить линейную зависимость или линейную независимость систем столбцов:

Решение. 1) Столбцы  линейно зависимы, так как можно составить нетривиальную линейную комбинацию, например, с коэффициентами
линейно зависимы, так как можно составить нетривиальную линейную комбинацию, например, с коэффициентами 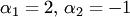 которая равна нулевому столбцу:
которая равна нулевому столбцу:  .
.
Столбцы 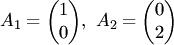 линейно независимы, так как равенство
линейно независимы, так как равенство  равносильное системе
равносильное системе  оказывается верным только при
оказывается верным только при  .
.
Свойства линейно зависимых и линейно независимых столбцов матриц.
Понятия линейной зависимости и линейной независимости определяются для строк и столбцов одинаково. Поэтому свойства, связанные с этими понятиями, сформулированные для столбцов, разумеется, справедливы и для строк.
1. Если в систему столбцов входит нулевой столбец, то она линейно зависима.
2. Если в системе столбцов имеется два равных столбца, то она линейно зависима.
3. Если в системе столбцов имеется два пропорциональных столбца  , то она линейно зависима.
, то она линейно зависима.
4. Система из 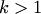 столбцов линейно зависима тогда и только тогда, когда хотя бы один из столбцов есть линейная комбинация остальных.
столбцов линейно зависима тогда и только тогда, когда хотя бы один из столбцов есть линейная комбинация остальных.
5. Любые столбцы, входящие в линейно независимую систему, образуют линейно независимую подсистему.
6. Система столбцов, содержащая линейно зависимую подсистему, линейно зависима.
7. Если система столбцов  — линейно независима, а после присоединения к ней столбца
— линейно независима, а после присоединения к ней столбца 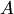 оказывается линейно зависимой, то столбец
оказывается линейно зависимой, то столбец 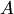 можно разложить по столбцам
можно разложить по столбцам  , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.
, и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.
22)
БАЗИС. КООРДИНАТЫ СТРОКИ В БАЗИСЕ.
Ба́ зис — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества - базисных векторов.
Любой декартовой системе координат на плоскости или в трехмерном пространстве может быть сопоставлен базис, состоящий из векторов, каждый из которых направлен вдоль своей координатной оси. Это относится и к прямоугольным декартовым координатам (тогда соответствующий базис называется ортогональным), так и к косоугольным декартовым координатам (которым будет соответствовать неортогональный базис).
Часто удобно выбрать длину каждого из базисных векторов единичной, такой базис называется нормированным.
Наиболее часто базис выбирают ортогональным и нормированным одновременно, тогда он называется ортонормированным.
В любом векторном пространстве базис можно выбрать различным образом (поменяв направления его векторов или их длины, например).
Представление какого-то конкретного или любого вектора пространства в виде линейной комбинации векторов базиса, например:
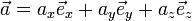 или
или  .
.
Числовые коэффициенты (ax, ay, az) называются коэффициентами разложения, а их набор в целом — представлением  вектора в базисе
вектора в базисе 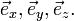 Разложение вектора по конкретному базису единственно; разложение одного и того же вектора по разным базисам — разное, то есть получается разный набор конкретных чисел, однако в результате при суммировании — как показано выше — дают один и тот же вектор.
Разложение вектора по конкретному базису единственно; разложение одного и того же вектора по разным базисам — разное, то есть получается разный набор конкретных чисел, однако в результате при суммировании — как показано выше — дают один и тот же вектор.
 .
.
23)
Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Ранг матрицы — Размерность образа dim (im (A)) линейного оператора, которому соответствует матрица.
Обычно ранг матрицы A обозначается  (
( ) или
) или  . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.
. Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.
Определение
Пусть 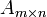 — прямоугольная матрица.
— прямоугольная матрица.
Тогда по определению рангом матрицы A является:
§ ноль, если A — нулевая матрица;
§ число  , где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к нему минор порядка (r + 1), если они существуют.
, где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к нему минор порядка (r + 1), если они существуют.
Теорема (о корректности определения рангов). Пусть все миноры матрицы 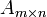 порядка k равны нулю (Mk = 0). Тогда порядка k равны нулю (Mk = 0). Тогда  , если они существуют. , если они существуют.
|
Определение 4.1.
Минором порядка k матрицы А называется определитель, составленный из элементов, стоящих на пересечении любых k строк и k столбцов данной матрицы.
Замечание. Таким образом, каждый элемент матрицы является ее минором 1-го порядка.
Определение 4.2. Ранг матрицы — это порядок ее наибольшего ненулевого минора.
Обозначения: r(A), R(A), Rang A.
Замечание. Очевидно, что значение ранга матрицы не может превышать меньшей из ее размерностей.
Примеры:
1., r(A)=0.
2.. Матрица В содержит единственный ненулевой элемент - являющийся минором 1-го порядка. Все определители более высоких порядков, составленные из элементов этой матрицы, будут содержать 0-ю строку и поэтому равны 0. Следовательно, r(B)=1.
3.. Единственным минором 3-го порядка является определитель матрицы С, но он равен 0, поскольку содержит пропорциональные столбцы. Следовательно, r(C)< 3.
Для того, чтобы доказать, что r(C)=2, достаточно указать хотя бы один минор 2-го порядка, не равный 0, например, Значит, r(C)=2.
4. следовательно, r(E)=3.
Замечание. Для матриц большой размерности непосредственное вычисление всех миноров затруднительно. Поэтому в этом случае можно преобразовать матрицу к так называемому треугольному виду (когда элементы, стоящие ниже равны 0), воспользовавшись операциями, не изменяющими ранг матрицы (эквивалентными преобразованиями). К ним относятся:
1) транспонирование
2) умножение строки на ненулевое число
3) перестановка строк
4) прибавление к элементам данной строки элементов любой другой строки, умноженных на ненулевое число
5) вычеркивание нулевой строки.
Действительно, любая из этих операций переводит нулевые миноры в нулевые, а ненулевые — в ненулевые. Матрица, полученная в результате, не равна исходной, но имеет тот же ранг.
Пример. Найдем ранг матрицы. Теоретически ранг этой матрицы может принимать значения от 1 до 4, так как из элементов матрицы можно создать миноры по 4-й порядок включительно. Но вместо того, чтобы вычислять все возможные миноры 4-го, 3-го и т.д. порядка, применим к матрице А эквивалентные преобразования. Вначале добьемся того, чтобы в первом столбце все элементы, кроме первого, равнялись 0. Для этого запишем вместо второй строки ее сумму с первой, а вместо третьей — разность третьей и удвоенной первой:
.
Затем из третьей строки вычтем вторую, а к четвертой прибавим вторую:
.
После вычеркивания нулевых строк получим матрицу размерности для которой максимальный порядок миноров, а, следовательно, и максимально возможное значение ранга равно 2:
.
Ее минор следовательно,